


Next: Spectral Test
Up: Statistical Tests
Previous: Lag- Autocorrelation
In this test, we examine a sequence of random numbers and record the lengths of successive ``complete sets'' of integers from 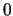 to
to 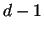 . In our implementation, it was not feasible to use
. In our implementation, it was not feasible to use 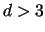 (this is because the Stirling Numbers of Second Kind get very large and produce overflow errors), so we examined complete sets of
(this is because the Stirling Numbers of Second Kind get very large and produce overflow errors), so we examined complete sets of 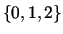 . At the conclusion of the algorithm, COUNT[r] represents the number of segments with with length r, for
. At the conclusion of the algorithm, COUNT[r] represents the number of segments with with length r, for  , and COUNT[t] is the number of segments with length
, and COUNT[t] is the number of segments with length 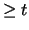 . For our experiments, we used
. For our experiments, we used 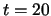 .
.
The next step is to compare the frequencies of occurrence with the expected frequencies. The expected probabilities are as follows.
Here
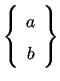 represents the Stirling's Number of Second Kind with parameters
represents the Stirling's Number of Second Kind with parameters 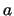 and
and 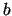 .
.
We apply the 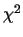 test to COUNT[d], COUNT[d+1],..., COUNT[t] with the degree of freedom,
test to COUNT[d], COUNT[d+1],..., COUNT[t] with the degree of freedom, 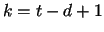 .
.
2001-05-30
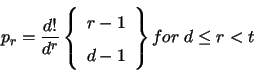
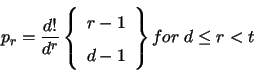

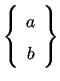 represents the Stirling's Number of Second Kind with parameters
represents the Stirling's Number of Second Kind with parameters ![]() and
and ![]() .
.
![]() test to COUNT[d], COUNT[d+1],..., COUNT[t] with the degree of freedom,
test to COUNT[d], COUNT[d+1],..., COUNT[t] with the degree of freedom, ![]() .
.