


Next: Birthday Spacings Test
Up: Statistical Tests
Previous: Coupon Collector's Test
Spectral Test
This test is devised to study the lattice structures of LCGs as mentioned in
Section 3.1, so it can not be applied to other families of RNGs.
According to Knuth in [8], this is by far the most powerful test
known, because it can fail LCGs which pass most statistical tests.
The IBM RANDU LCG (with parameters
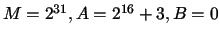 ) fails in this
test for 3 dimensions and above (see Figure 2.)
) fails in this
test for 3 dimensions and above (see Figure 2.)
The theory behind the spectral test algorithm
is quite complicated; it suffices to say that the goal is to determine the
value of
subject to
where 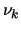 is the inverse of
is the inverse of 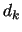 .
.
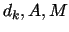 , and
, and 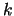 have the same meanings as in Section 3.1.
have the same meanings as in Section 3.1.
Any good LCG should have high values for each 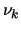 . Theoretical
value of
. Theoretical
value of 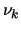 is
is 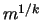 where
where 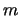 is the period length.
With spectral test, we can estimate the how worse the lattice structure
will be without plotting millions of samples. IBM RANDU LCG has
is the period length.
With spectral test, we can estimate the how worse the lattice structure
will be without plotting millions of samples. IBM RANDU LCG has
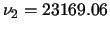 , which is good, but
, which is good, but 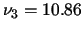 , which is much less
than theoretical value 812.75. The maximum distance between the hyperplanes
in Figure 2 is thus as large as
, which is much less
than theoretical value 812.75. The maximum distance between the hyperplanes
in Figure 2 is thus as large as
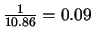 .
.
Our spectral test code is an exact implementation of the algorithm given in
[8].



Next: Birthday Spacings Test
Up: Statistical Tests
Previous: Coupon Collector's Test
2001-05-30
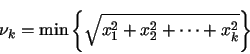
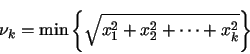
![]() . Theoretical
value of
. Theoretical
value of ![]() is
is ![]() where
where ![]() is the period length.
With spectral test, we can estimate the how worse the lattice structure
will be without plotting millions of samples. IBM RANDU LCG has
is the period length.
With spectral test, we can estimate the how worse the lattice structure
will be without plotting millions of samples. IBM RANDU LCG has
![]() , which is good, but
, which is good, but ![]() , which is much less
than theoretical value 812.75. The maximum distance between the hyperplanes
in Figure 2 is thus as large as
, which is much less
than theoretical value 812.75. The maximum distance between the hyperplanes
in Figure 2 is thus as large as
![]() .
.