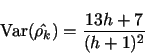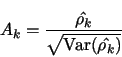Next: Coupon Collector's Test
Up: Statistical Tests
Previous: Runs Test
This empirical test directly assesses the degree of independence of samples.
As pointed out in Section 2.1, if the samples are independently
and identically distributed (IID) random variables,
the autocorrelation should be 0.
The lag-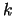 autocorrelation statistic
autocorrelation statistic  of samples
of samples
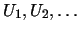 is defined as
is defined as
where
and 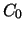 is the sample variance. If
is the sample variance. If 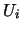 's are uniformly
distributed,
's are uniformly
distributed,
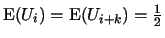 ,
,
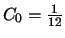 .
Then we have
.
Then we have
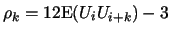 .
.
In practice, we do not calculate  directly; instead, an estimate of
directly; instead, an estimate of
 can be obtained by just plugging
can be obtained by just plugging  ,
, 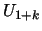 ,
, 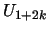 ,
,  into
following formula as shown in [10]:
into
following formula as shown in [10]:
where
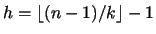 . If we further assume that
. If we further assume that 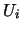 's are independent,
then we have
's are independent,
then we have
Under the null hypothesis that  (independence), the following
statistic has an approximate standard normal distribution
(independence), the following
statistic has an approximate standard normal distribution
The hypothesis will be rejected at significance level 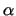 if
if
 .
. 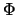 is the distribution function of
standard normal distribution.
is the distribution function of
standard normal distribution.
In this project we have tested up to 10-lag autocorrelation of each RNG.



Next: Coupon Collector's Test
Up: Statistical Tests
Previous: Runs Test
2001-05-30
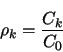
![]() directly; instead, an estimate of
directly; instead, an estimate of
![]() can be obtained by just plugging
can be obtained by just plugging ![]() ,
, ![]() ,
, ![]() ,
, ![]() into
following formula as shown in [10]:
into
following formula as shown in [10]: