


Next: Lag- Autocorrelation
Up: Statistical Tests
Previous: Permutation Test
A ``run'' refers to a succession of similar events separated by different events.
In this test a ``run-up'' is a monotonically increasing subsequence and a ``run-down''
is a monotonically decreasing subsequence. Consider the sequence (3,1,4,1,5,9,2,6,5,3,5).
By putting bars between runs-up, we have
 . It exhibits two runs-up of
length 1, three runs-up of length 2 and one run-up of length 3. Intuitively, runs of longer
lengths should be rare if the samples are random, so this test measures the randomness by
examining the distribution of lengths of runs up and runs down. Unlike the permutation test
in Section 4.4, we can not directly apply the
. It exhibits two runs-up of
length 1, three runs-up of length 2 and one run-up of length 3. Intuitively, runs of longer
lengths should be rare if the samples are random, so this test measures the randomness by
examining the distribution of lengths of runs up and runs down. Unlike the permutation test
in Section 4.4, we can not directly apply the 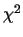 test on it since
adjacent runs are not independent. Instead, the following statistic is computed
test on it since
adjacent runs are not independent. Instead, the following statistic is computed
where  is number of samples and
is number of samples and ![$\mbox{RUN}[i]$](img163.gif) stores the number of runs of length
stores the number of runs of length 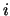 .
.
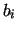 and
and 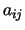 are given in [8]. Note that runs of length greater than 6
are considered to be 6 in the test.
are given in [8]. Note that runs of length greater than 6
are considered to be 6 in the test.
When  is large (
is large (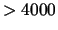 ),
),  has
has 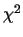 distribution with 6 degrees of freedom
under the hypothesis that the samples are independent, uniform random variates.
In this project we carried out both runs-up and runs-down tests on the RNGs. Other
kinds of runs tests like runs above and below the mean are also devised,
distribution with 6 degrees of freedom
under the hypothesis that the samples are independent, uniform random variates.
In this project we carried out both runs-up and runs-down tests on the RNGs. Other
kinds of runs tests like runs above and below the mean are also devised,



Next: Lag- Autocorrelation
Up: Statistical Tests
Previous: Permutation Test
2001-05-30
![\begin{displaymath}
V = \frac{1}{N} \sum_{1 \le i,j \le 6} (\mbox{RUN}[i]-Nb_i)(\mbox{RUN}[j]-Nb_j)a_{ij}
\end{displaymath}](img162.gif)
![\begin{displaymath}
V = \frac{1}{N} \sum_{1 \le i,j \le 6} (\mbox{RUN}[i]-Nb_i)(\mbox{RUN}[j]-Nb_j)a_{ij}
\end{displaymath}](img162.gif)
![]() is large (
is large (![]() ),
), ![]() has
has ![]() distribution with 6 degrees of freedom
under the hypothesis that the samples are independent, uniform random variates.
In this project we carried out both runs-up and runs-down tests on the RNGs. Other
kinds of runs tests like runs above and below the mean are also devised,
distribution with 6 degrees of freedom
under the hypothesis that the samples are independent, uniform random variates.
In this project we carried out both runs-up and runs-down tests on the RNGs. Other
kinds of runs tests like runs above and below the mean are also devised,