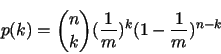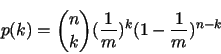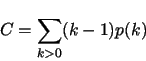Next: Permutation Test
Up: Statistical Tests
Previous: Kolmogorov-Smirnov Test
The 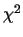 test statistic is meaningful only when each interval has more than
5 samples, but this test is designed such that the number of intervals
are much larger than number of samples [8].
Suppose we throw
test statistic is meaningful only when each interval has more than
5 samples, but this test is designed such that the number of intervals
are much larger than number of samples [8].
Suppose we throw 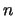 balls at random into
balls at random into  empty urns with
empty urns with  ,
then we say a collision occurs if the ball falls into an nonempty urn.
Theoretically, the probability that an urn receives exactly
,
then we say a collision occurs if the ball falls into an nonempty urn.
Theoretically, the probability that an urn receives exactly 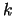 balls
is
balls
is
so the expected number of collisions is
When  ,
,
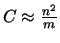 . In the experiment, we use
. In the experiment, we use 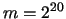 and
and 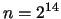 , so the observed number of collisions should be very close to
, so the observed number of collisions should be very close to
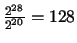 .
.
2001-05-30