


Next: Collision Test
Up: Statistical Tests
Previous: Test
The main problem with 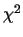 test is the choice of number and size of the intervals.
Although rules of thumb can help produce good results (for example, the range should
be divided such that
test is the choice of number and size of the intervals.
Although rules of thumb can help produce good results (for example, the range should
be divided such that
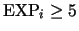 for all
for all 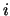 ), there is no panacea
for all kinds of applications [10].
Another problem is that the
), there is no panacea
for all kinds of applications [10].
Another problem is that the 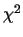 test is designed for discrete distributions, so
in continuous case the
test is designed for discrete distributions, so
in continuous case the 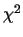 test statistic is only an approximation [7].
test statistic is only an approximation [7].
Kolmogorov-Smirnov (KS) test is designed to address above issues. Given the
hypothesized continuous distribution function 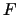 without jumps, this test compares
without jumps, this test compares
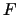 to the empirical distribution function,
to the empirical distribution function, 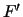 , of the samples. The KS test
statistic
, of the samples. The KS test
statistic 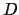 is the largest absolute deviation between
is the largest absolute deviation between 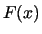 and
and 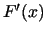 over the
range of the random variable:
over the
range of the random variable:
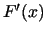 is defined as
is defined as
where  is the number of samples. For testing against a uniform distribution, we
must first sort the samples into ascending order
is the number of samples. For testing against a uniform distribution, we
must first sort the samples into ascending order
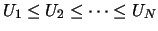 ,
(
,
(
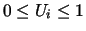 for all
for all 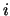 ) then computer the following statistics
) then computer the following statistics
Then
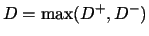 . To assess
. To assess 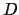 , we use the hypothesis test as mentioned in
Section 4.1.
, we use the hypothesis test as mentioned in
Section 4.1. 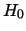 will be rejected at significance level
will be rejected at significance level 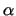 if
if
where values of 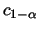 are given by the following table:
are given by the following table:
Since KS-test does not group samples into categories, it is more sensitive to
outliers. In this sense, KS test makes better use of each sample and is more
precise than the 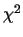 test.
test.



Next: Collision Test
Up: Statistical Tests
Previous: Test
2001-05-30
![]() without jumps, this test compares
without jumps, this test compares
![]() to the empirical distribution function,
to the empirical distribution function, ![]() , of the samples. The KS test
statistic
, of the samples. The KS test
statistic ![]() is the largest absolute deviation between
is the largest absolute deviation between ![]() and
and ![]() over the
range of the random variable:
over the
range of the random variable:
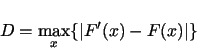
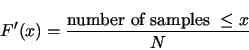
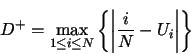
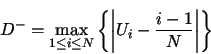
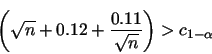

![]() test.
test.