$\chi ^2$ Test

$\chi ^2$ test is used to estimate the uniformity of a random sequence in this project. It is actually a general purpose goodness-of-fit test which can assess whether the observations are from the hypothesized distribution. To calculate the $\chi ^2$ test statistic in either discrete or continuous distribution case, we prepare a histogram of the observed data by dividing the range of data into $k$ adjacent intervals and tallying number of observed data $\mbox{OBS}_i$ in each interval $i$. Then we use the following statistic

$$K^2 = \sum_{i=1}^{k} \frac{(\mbox{EXP}_i-\mbox{OBS}_i)^2}{\mbox{EXP}_i}$$

where $\mbox{EXP}_i$ denotes the expected number of samples in interval $i$ , which is calculated from $F$ and total number of samples $n$. A perfect fit would have $K^2 = 0$, but in most cases $K^2$ is nonzero. When $n$ is large, $K^2$ converges in distribution to a $\chi ^2$ distribution with $k-1$ degree of freedom (df). To assess whether $K^2$ is really a $\chi ^2$ distribution with the given df, we must set up a hypothesis test as follows. The null hypothesis $H_0$ is that the observations are from $\chi ^2$ distribution with df=$k-1$. A test with significance level $\alpha$ will reject $H_0$ if $K^2 > \chi^2_{k-1,1-\alpha}$. As it turns out, the larger the $\alpha$, the more stringent the test since $\chi^2_{k-1,1-\alpha}$ is smaller.

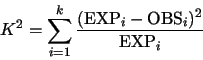
In this project we have assessed the 1-distributed, 2-distributed, and 3-distributed properties of each RNG. A $d$-distributed test is to estimate the $d$-dimensional uniformity as mentioned in Section $\ref{sec:infdist}$. For 1-distributed, $[0,1)$ is divided into 4096 equidistant intervals. For 2-distributed, the unit square is divided into 64x64 equal sized cells. For 3-distributed, the unit cube is divided into 16x16x16 equal sized cells. The tests for higher than one dimensional uniformity are carried out exactly the same as for the one dimensional $\chi ^2$ case. All of these tests are compared with $\chi ^2$ distribution with df=4095.

One closely related test called serial test is to use non-overlapping $d$-dimensional points $(U_{nd+1}$, $U_{nd+2}$, ..., $U_{nd+d})$, $n=0, 1, \ldots$. To differentiate between these tests, in our experiments we call the tests discussed in the previous paragraph ``1-D $\chi ^2$ test'', ``2-D $\chi ^2$ test (overlapping)'', and ``3-D $\chi ^2$ test (overlapping)'', and serial tests are ``2-D $\chi ^2$ test (non-overlapping)'' and ``3-D $\chi ^2$ test (non-overlapping)''.

In both cases, if the samples have high autocorrelation, the distribution of $d$-dimensional points will deviates greatly from $d$-dimensional uniformity for $d>1$. So higher dimensional uniformity tests also provide an indirect check of the assumption that the samples are independent.