8.6.0.14
Lab 13: Accumulators and generative recursion
Remember to follow
(and when necessary, adapt)
the design recipe for each function.
When you write a generative recursive function, you must
provide a termination argument.
When you write a function using an accumulator, you must
provide an accumulator statement.
1 Accumulators

This section is all about accumulators.
There is no generative recursion in this section.
When you write a function using an accumulator, you must
provide an accumulator statement.
Let’s review a simple example. Assume you have a list of numbers
and you want to calculate the sum of those numbers. You have learned
many ways of doing this already; here it is done using an accumulator.
| ; sum : [ListOf Number] -> Number |
| ; sums the numbers in the given list |
| (define (sum lon) |
| (local [; sum/a : [ListOf Number] Number -> Number |
| ; adds the numbers in the list one by one to the second argument |
| ; *Accumulator*: sum-so-far is the sum of numbers seen so far |
| ; |
| ; examples: |
| ; lon sum-so-far output |
| ; ------------------------------------------------------ |
| ; (list 1 2 3 4 5) 0 (+ 0 1 2 3 4 5) |
| ; (list 2 3 4 5) 0 + 1 = 1 (+ 0 1 2 3 4 5) |
| ; (list 3 4 5) 1 + 2 = 3 (+ 0 1 2 3 4 5) |
| ; (list 4 5) 3 + 3 = 6 (+ 0 1 2 3 4 5) |
| ; (list 5) 6 + 4 = 10 (+ 0 1 2 3 4 5) |
| ; empty 10 + 5 = 15 (+ 0 1 2 3 4 5) |
| ; |
| (define (sum/a lon sum-so-far) |
| (cond [(empty? lon) sum-so-far] |
| [else (sum/a (rest lon) |
| (+ (first lon) sum-so-far))]))] |
| (sum/a lon 0))) |
| (check-expect (sum (list 1 2 3 4 5)) (+ 0 1 2 3 4 5)) |
Note that every such function will have a helper written using an
accumulator. Both the original function sum
and the helper sum/a need
their signatures and purpose statements clearly indicated. For
every function using an accumulator, we need to clearly
identify the accumulator and write an accumulator statement.
An accumulator statement should explain what the accumulator is,
not how to use or change the accumulator.
As usual, we also need to write examples for every function.
A function using an accumulator should have many examples,
because each time the original function is used once, the
helper is used many times. In the function sum above,
all the examples for sum/a arise from the one and only
example for sum. Each example for sum/a shows
the list being processed and the accumulator being updated.
Exercise 1. The sum/a function above is defined
locally. Convert it to a top-level definition and convert
all the examples to tests. Write a new test for sum
and write all the corresponding tests for sum/a.
For each remaining exercise in this lab, we describe a strategy for using
an accumulator. Your job is to design a helper function that uses an
accumulator in the way we describe. You also need to design an original
function that calls the helper function and passes the initial accumulator
value.
Exercise 2.
Design a function alternating-sum to compute the alternating sum
of all elements in a list of numbers.
Your helper function should use accumulators in the following way:
(We have provided the accumulator statements.)
| ; *Accumulator*: subtract is whether to subtract rather than add the next number |
| ; *Accumulator*: sum-so-far is the sum of numbers seen so far |
| ; examples: |
| ; numbers subtract sum-so-far output |
| ; ---------------------------------------------------------------------- |
| ; (list 1 4 9 16 9 7 4 9 11) false 0 -2 |
| ; (list 4 9 16 9 7 4 9 11) true 0 + 1 = 1 -2 |
| ; (list 9 16 9 7 4 9 11) false 1 - 4 = -3 -2 |
| ; (list 16 9 7 4 9 11) true -3 + 9 = 6 -2 |
| ; (list 9 7 4 9 11) false 6 - 16 = -10 -2 |
| ; (list 7 4 9 11) true -10 + 9 = -1 -2 |
| ; (list 4 9 11) false -1 - 7 = -8 -2 |
| ; (list 9 11) true -8 + 4 = -4 -2 |
| ; (list 11) false -4 - 9 = -13 -2 |
| ; empty true -13 + 11 = -2 -2 |
So, do not use generative recursion; stick with structural recursion and follow
the template for processing a list of numbers.
Exercise 3.
Design a function funky that takes a [ListOf 1String]
as input and produces the same [ListOf 1String] as output,
except the output should alternate between upper-case and lower-case.
Your helper function should use an accumulator in the following way:
(You must provide an accumulator statement.)
| ; examples: |
| ; letters capitalize output |
| ; ------------------------------------------------------------------------------ |
| ; (explode "Computer Science") true (explode "CoMpUtEr sCiEnCe") |
| ; (explode "omputer Science") false (explode "oMpUtEr sCiEnCe") |
| ; (explode "mputer Science") true (explode "MpUtEr sCiEnCe") |
| ; (explode "puter Science") false (explode "pUtEr sCiEnCe") |
| ; (explode "uter Science") true (explode "UtEr sCiEnCe") |
| ; (explode "ter Science") false (explode "tEr sCiEnCe") |
| ; (explode "er Science") true (explode "Er sCiEnCe") |
| ; (explode "r Science") false (explode "r sCiEnCe") |
| ; (explode " Science") true (explode " sCiEnCe") |
| ; (explode "Science") false (explode "sCiEnCe") |
| ; (explode "cience") true (explode "CiEnCe") |
| ; (explode "ience") false (explode "iEnCe") |
| ; (explode "ence") true (explode "EnCe") |
| ; (explode "nce") false (explode "nCe") |
| ; (explode "ce") true (explode "Ce") |
| ; (explode "e") false (explode "e") |
| ; (explode "") true (explode "") |
So, do not use generative recursion; stick with structural recursion and follow
the template for processing a
[ListOf 1String].
Use
string-upcase,
string-downcase, and
not.
Exercise 4.
Design a function sentence that takes a [ListOf 1String]
as input and produces the same [ListOf 1String] as output,
except the first 1String should become upper-case, and
whenever a period appears, the next non-whitespace 1String
should also become upper-case. This process is like how automatic
capitalization works on some keyboards.
Your helper function should use an accumulator in the following way:
(You must provide an accumulator statement.)
| ; examples: |
| ; letters capitalize output |
| ; ------------------------------------------------------------------------ |
| ; (explode "hey. whats up") true (explode "Hey. Whats up") |
| ; (explode "ey. whats up") false (explode "ey. Whats up") |
| ; (explode "y. whats up") false (explode "y. Whats up") |
| ; (explode ". whats up") false (explode ". Whats up") |
| ; (explode " whats up") true (explode " Whats up") |
| ; (explode "whats up") true (explode "Whats up") |
| ; (explode "hats up") false (explode "hats up") |
| ; (explode "ats up") false (explode "ats up") |
| ; (explode "ts up") false (explode "ts up") |
| ; (explode "s up") false (explode "s up") |
| ; (explode " up") false (explode " up") |
| ; (explode "up") false (explode "up") |
| ; (explode "p") false (explode "p") |
| ; (explode "") false (explode "") |
So, do not use generative recursion; stick with structural recursion and follow
the template for processing a
[ListOf 1String].
Use
string-upcase and
string-whitespace?.
Exercise 5.
Interpret a list of numbers as a sequence of deposit and withdrawal
transactions in the same bank account, ordered from oldest to newest. Design a
function overdrawn? that takes such a list as input, starting with
opening the account, and returns a boolean that says whether the account
balance ever becomes negative at any point in the history of the account.
Use an accumulator that is the current account balance.
2 Generative terrain

This section is all about generative recursion.
There is no accumulator in this section.
When you write a generative recursive function, you must
provide a termination argument.
In this section, you’ll design a program to generate random terrain like
this:
You will use generative recursion: given two points p and q to
connect, your program will decompose the problem of connecting p to q
into the problem of connecting p to r and the problem of connecting
r to q. Here r is almost the midpoint of p and q, but
randomly moved a little bit.
Such a decomposition can be expressed using a CurveTree:
| ; A CurveTree is one of: |
| ; - (make-segment Posn Posn) |
| ; - (make-connect CurveTree CurveTree) |
| (define-struct segment [p1 p2]) |
| (define-struct connect [c1 c2]) |
Exercise 6.
Here is a typical function that processes a CurveTree:
| (require 2htdp/image) |
| ; draw-curve-tree : CurveTree Image -> Image |
| ; Draw the given CurveTree on the given image |
| (define (draw-curve-tree c i) |
| (cond [(segment? c) |
| (scene+line i |
| (posn-x (segment-p1 c)) |
| (posn-y (segment-p1 c)) |
| (posn-x (segment-p2 c)) |
| (posn-y (segment-p2 c)) |
| "blue")] |
| [(connect? c) |
| (draw-curve-tree (connect-c1 c) |
| (draw-curve-tree (connect-c2 c) |
| i))])) |
Write an example for draw-curve-tree with at least 3 segments.
Exercise 7.
Design a function midpoint that takes two Posns as input and
returns the Posn that is their midpoint.
Exercise 8.
Design a function almost-midpoint that takes two Posns and two
Numbers as input and returns the Posn that is almost the midpoint
of the given Posns, except with the given Numbers added to the X
and Y coordinates.
Exercise 9.
Here is a handy function:
| ; drift : Number -> Number |
| ; pick a random number between (- amount) and amount |
| (check-random (drift 5) (- (/ (random 10001) 1000) 5)) |
| (define (drift amount) |
| (* amount (- (/ (random 10001) 5000) 1))) |
Study the signature and purpose of this function, then try it out in the
Interactions Window.
How does (drift 100) behave differently from (drift 2)?
Exercise 10.
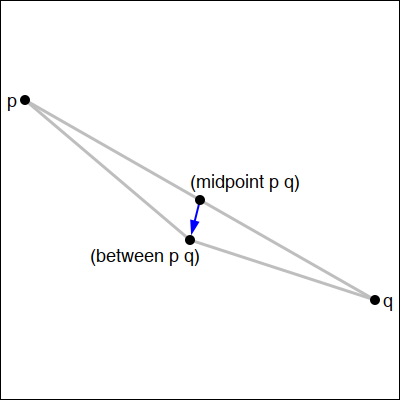
Design a function between that takes two Posns as input and
returns a Posn that is almost their midpoint, but randomly moved a
little bit. The picture below illustrates the difference between the functions
midpoint and between.
The distance of random movement must be proportional to the
distance between the two inputs, so use
(drift (* 0.2 (dist ... ...))) twice, once to move the
x coordinate and once to move the y coordinate.
So use dist, drift, and almost-midpoint.
Exercise 11.
Finally, design a function to generate a random terrain.
| ; generate-terrain : Posn Posn -> CurveTree |
| ; generate a random terrain connecting the two given points |
| ; *Termination*: ??? |
| (define (generate-terrain p q) |
| (cond [??? |
| (make-segment ??? ???)] |
| [else |
| (local [; r : Posn |
| (define r (between p q))] |
| (make-connect (generate-terrain ??? ???) |
| (generate-terrain ??? ???)))])) |
Again, use generative recursion: if
p and
q are not close, then
decompose the problem of connecting
p to
q into the problem of
connecting
p to
r and the problem of connecting
r to
q. To
check if p and q are close, you can use
dist. You don’t have to test
this function
generate-terrain using
check-expect or
check-random, but do try it out using
draw-curve-tree!