Physically Realizable Quantum Algorithms
Quantum computers (QCs) rely on concepts such as superposition and entanglement for sophisticated information processing.
They have the potential to process information, perform optimizations and recognize patterns that are impossible or computationally hard for their classical counterparts.
Reaching this potential requires physically realizable quantum algorithms that are scalable, tolerant to infidelities (near-term era), and in compliance with the quantum mechanical postulates.
The purpose of this study is to develop and analyze quantum algorithms harnessing these potentials.
Randomized Quantum Stochastic Gradient Descent
Gradient decent is an iterative approach for classical optimization, where at each iteration the set of parameters are shifted toward the negative of the gradient of the objective function as
$$\overrightarrow{a}_{t+1}=\overrightarrow{a}_{t}-\eta_t \nabla L(\overrightarrow{a}_{t})$$
In quantum settings, however, gradient computation is prohibitive because of the stochasticity quantum measurements. Current solutions rely on approximating the gradient with repeated measurements of several copies of each quantum state. As a result such approaches often have a high copy complexity for training a QNN with large number of parameters.
This project proposes randomized QSGD as a novel solution without the need for repeated measurements. Instead of approximating the gradient, randomized QSGD relies on an unbiased gradient measurement, which statistically points to the gradient's direction over a time interval. The update rule in this approach is of the form
$$\overrightarrow{a}_{t+1}=\overrightarrow{a}_{t}-\eta_t Z_t$$
where \(Z_t\) is a random vector as the output of an unbiased gradient measurement. This approach eliminates the need for sample duplication, hence consistent with the no-cloning rule as each sample is processed only once per epoch.
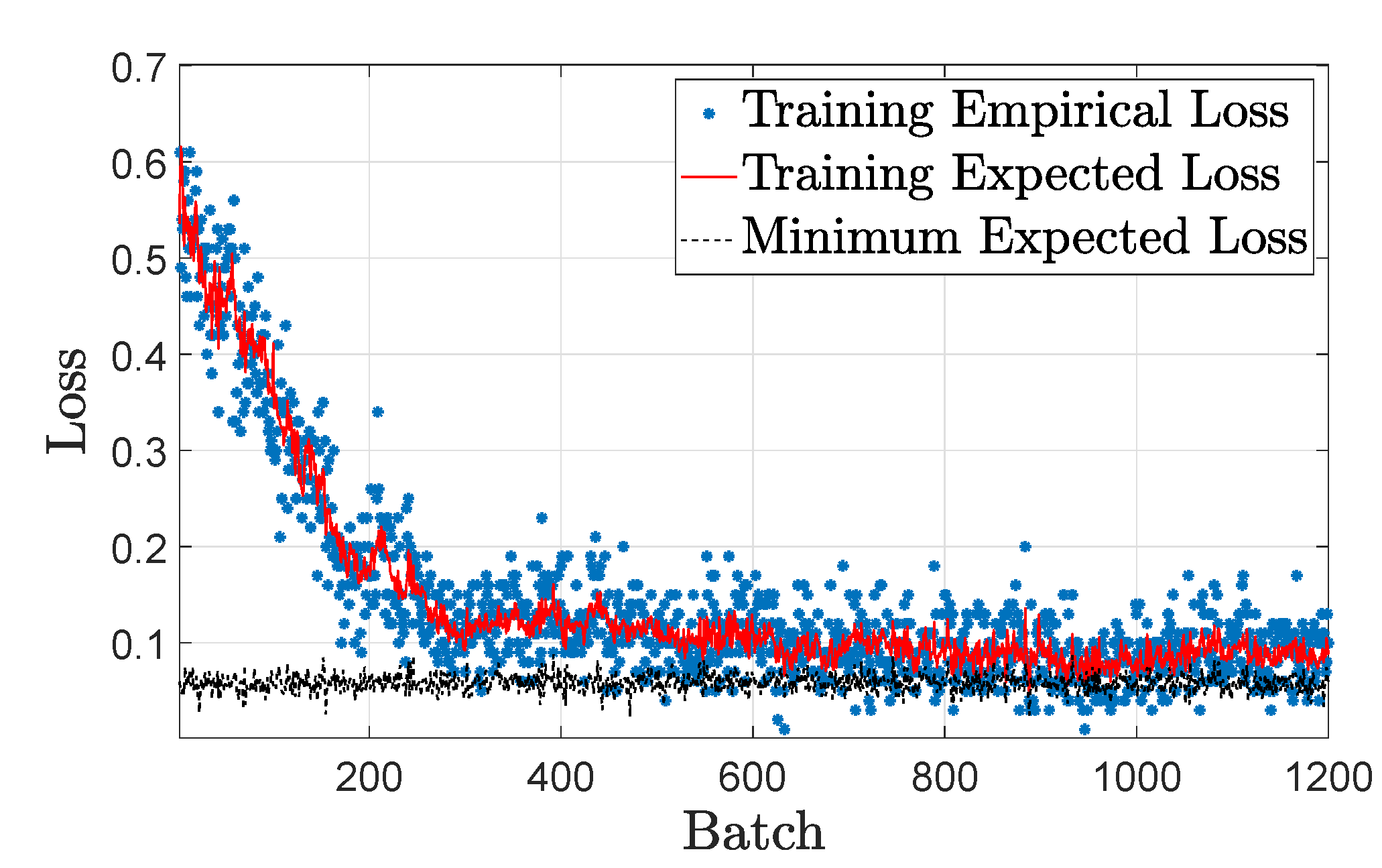
Training loss with the randomized QSGD
Band limited Quantum Neural Networks (QNNs):
Quantum neural networks (QNNs), broadly regarded as the quantum analog of neural networks, consist of a network of small computation
unites as quantum perceptrons. Each QP can be viewed as a small quantum circuit with a set of parameters to be tuned.

A generic feedforward QNN
The training procedures for QNNs pose significant computational challenges over and above classical neural networks due to their exponential parameter space.
This work introduces a new model for QNNs that relies on band-limited Fourier expansions of transfer functions of QP to design scalable training.
This approach relies on the Pauli decomposition of quantum operators to control the circuit depth of QPs in a QNN.
With a narrow power spectrum, we show that the proposed QPs provide the basis for robustness to gate infidelity.
Moreover, we adopt QSGD for the efficient training of QNNs.
Theory of Quantum Learning
This research aims to study learning in quantum environments with applications in quantum state classification/discrimination.
In this model, there are unknown quantum states with classical labels.
The objective is to accurately learn the labeling law by processing a set of \(n\) training samples \((\rho_i, y_i)\) drawn based on an unknown but fixed distribution \(D\).
The quantum nature of the problem leads to a series of unique properties such as no-cloning, sample collapse, and measurement indeterminism.
This research aims to study the effect of these properties from a learning theoretic perspective and to develop fundamental limits of learning in quantum (i.e., quantum sample complexity).
We seek to answer the following questions:
What are the quantum complexity measures as counterparts of classical measures such as VC-dimension and Rademacher complexity?
Classical Machine Learning:
Feature Selection via Discrete Fourier Expansion
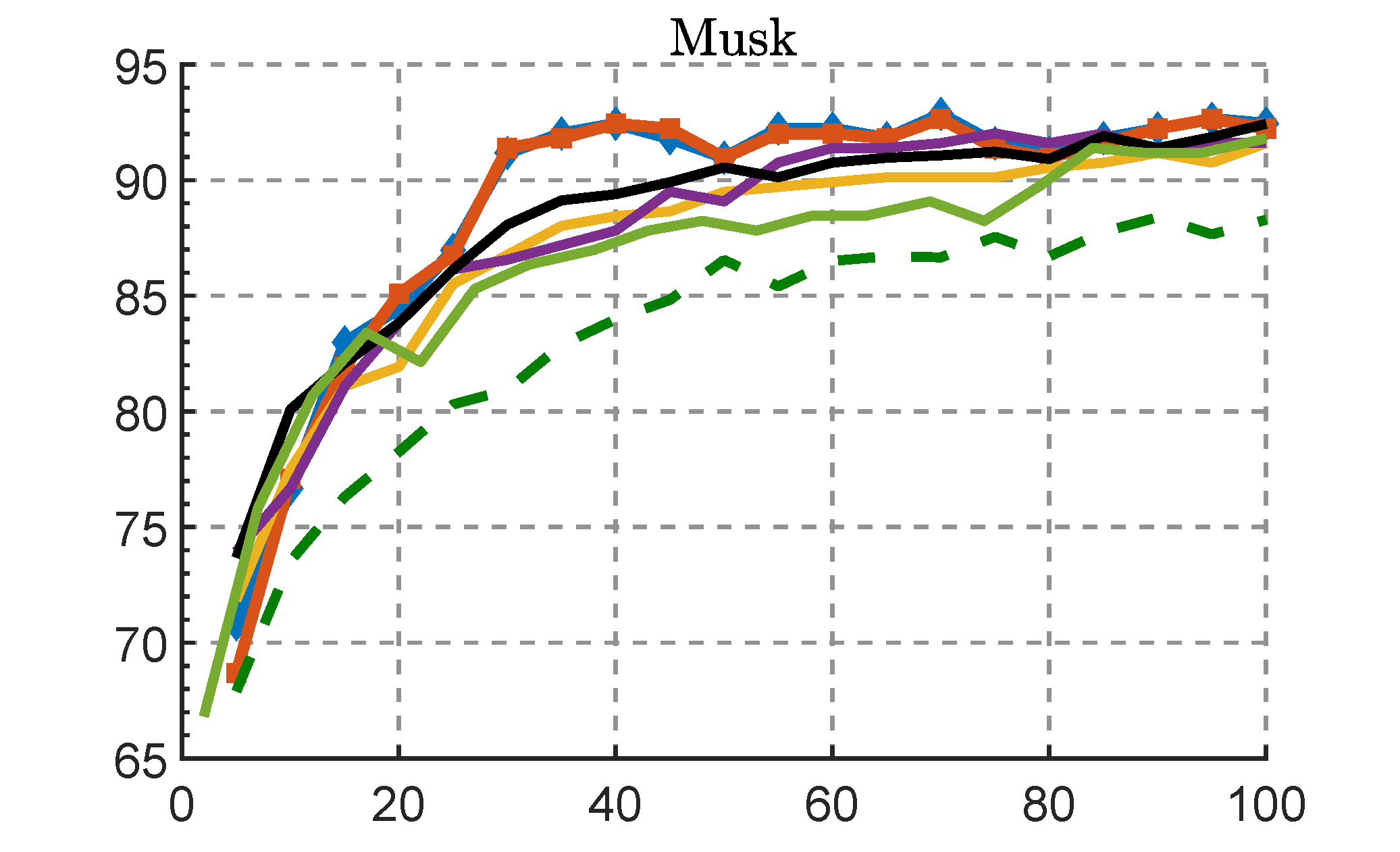
Classification accuracy vs the number of selected features
Feature selection (FS) plays a pivotal role in removing statistical redundancies, especially when model interpretability and knowledge extraction are essential.
However, conventional methods (e.g., Pearson and Fisher score) capture only linear relations or focus on the effect of individual features instead of subsets of features.
This project takes an alternative perspective and introduces feature selection based on discrete Fourier analysis to capture nonlinear relations with low sample complexity.
We reformulate the feature selection problem in the Fourier domain and develop a computationally efficient measure for selecting feature subsets.
We demonstrate that this measure finds provably asymptotically optimal feature subsets by connecting the Bayesian error rate with the Fourier coefficients.
Furthermore, we implement this measure with a search algorithm and introduce a feature selection algorithm for finding the most relevant features.
Quantum Information Theory:Faithfull Simulation of Quantum Measurements
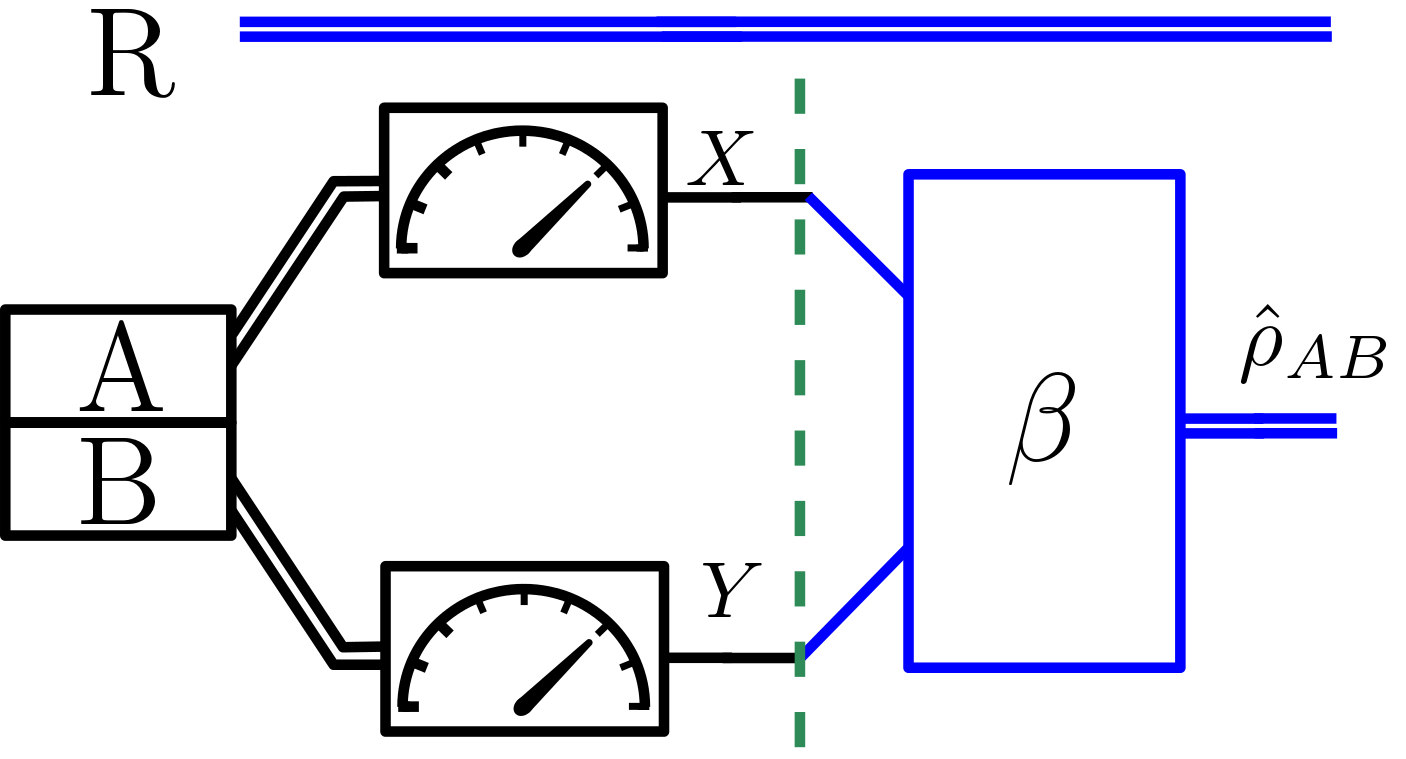
Simulating locally separated quatnum measurements.
This work is motivated by the current technological difficulties in quantum information and has experimental and theoretical applications.
LOCC is a well-known solution aiming at implementing quantum operations locally.
In this approach, a multipartite quantum system is distributed to various parties, each restricted to acting locally on their respective subsystems by performing measurements and quantum operations.
The parties are free to communicate any classical data, including shared randomness.
This project focuses on the fundamental limits of the classical resources in LOCC for quantum measurements.
In a two-user setting, a bipartite quantum system AB is locally available at two separate agents.
The goal is to replicate the outcome of a joint measurement M on AB with local operations.
The agents measure their subsystems locally and send classical bits to a receiving party.
The objective is to arrive at an estimation that is statistically indistinguishable from the true outcome of M (a.k.a faithful simulation).




