


Next: Random Number Generators
Up: Randomness Assessments
Previous: Unpredictable
Kolmogorov Complexity
In Shannon's information theory, the degree of randomness of a finite sequence
of discrete values can be quantified by calculating the entropy (``amount of information'')
as
where  is the probability of occurrences of value
is the probability of occurrences of value 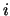 . Using this criterion, the higher
the entropy, the more the randomness. For instance, the sequence 00100010
(entropy=
. Using this criterion, the higher
the entropy, the more the randomness. For instance, the sequence 00100010
(entropy=
 ) is less random
than 01010101 (entropy =
) is less random
than 01010101 (entropy =
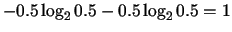 )
The inadequacy of Shannon's measure of randomness is apparent, because
intuitively the former sequence is more random than the latter. To remedy this problem,
Kolmogorov complexity (also called descriptional complexity [13])
takes into account the order of each number in the sequence. Without
loss of generality, assume the sequence in discussion is a finite sequence of bits
represented by its decimal value
)
The inadequacy of Shannon's measure of randomness is apparent, because
intuitively the former sequence is more random than the latter. To remedy this problem,
Kolmogorov complexity (also called descriptional complexity [13])
takes into account the order of each number in the sequence. Without
loss of generality, assume the sequence in discussion is a finite sequence of bits
represented by its decimal value 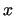 . Then, informally, the Kolmogorov complexity
. Then, informally, the Kolmogorov complexity
 maps
maps 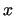 to a number which is the length of the shortest
program (written in a fixed programming language) that generates it. We say a sequence
to a number which is the length of the shortest
program (written in a fixed programming language) that generates it. We say a sequence
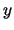 is random or incompressible if
is random or incompressible if 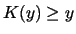 , because the only way to describe or
reproduce
, because the only way to describe or
reproduce 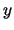 is to put
is to put 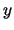 in the program.
in the program.
From this point of view, sequences produced by any RNG and the decimal expansions of
irrational numbers like 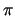 are not random since their lengths are much longer
than the programs that output
them. This also coincides with the notion that algorithmic RNGs are only pseudorandom.
Although Kolmogorov complexity captures the concept of randomness well,
it is proven to be uncomputable (i.e. undecidable), therefore, there is no practical
value of using it to assess the quality of RNGs.
are not random since their lengths are much longer
than the programs that output
them. This also coincides with the notion that algorithmic RNGs are only pseudorandom.
Although Kolmogorov complexity captures the concept of randomness well,
it is proven to be uncomputable (i.e. undecidable), therefore, there is no practical
value of using it to assess the quality of RNGs.



Next: Random Number Generators
Up: Randomness Assessments
Previous: Unpredictable
2001-05-30
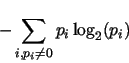
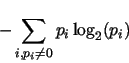
![]() are not random since their lengths are much longer
than the programs that output
them. This also coincides with the notion that algorithmic RNGs are only pseudorandom.
Although Kolmogorov complexity captures the concept of randomness well,
it is proven to be uncomputable (i.e. undecidable), therefore, there is no practical
value of using it to assess the quality of RNGs.
are not random since their lengths are much longer
than the programs that output
them. This also coincides with the notion that algorithmic RNGs are only pseudorandom.
Although Kolmogorov complexity captures the concept of randomness well,
it is proven to be uncomputable (i.e. undecidable), therefore, there is no practical
value of using it to assess the quality of RNGs.