


Next: Kolmogorov Complexity
Up: Randomness Assessments
Previous: -distributed
Unpredictable
In the context of cryptography, a number is random if it can not be predicted by
observing previous generated numbers, even with infinite computing resources.
Informally, an RNG is polynomial-time (PT) perfect or unpredictable if the time
required to predict its next output is super-polynomial (e.g. exponential) or
the probability of correct prediction in polynomial-time is the same as randomly
guessing a value. Unpredictability must be specified in terms of some kind of
resource bounds since RNGs are just finite, deterministic algorithms. For example,
if we know the random sequence is generated by an RNG whose program length is 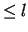 ,
we can exert all conceivable computing powers to
enumerate all programs of length
,
we can exert all conceivable computing powers to
enumerate all programs of length 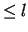 (there are only finitely many of them),
compare their outputs with observed values, and hence extrapolate the output.
(there are only finitely many of them),
compare their outputs with observed values, and hence extrapolate the output.
PT unpredictable RNGs are usually based on the intractability of
NP problems such as ``integer factoring'' or ``discrete logarithm.''
The former is to find nontrivial factors of a larger integer,
while the latter is to evaluate the value of
 where
where 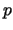 is a prime and
is a prime and 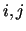 are integers greater than 1. For example,
are integers greater than 1. For example,
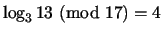 because
because
 .
As long as the famous debate of P
.
As long as the famous debate of P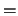 NP is unsettled, they can
still claim to be cryptographically secure in polynomial-time sense.
More details on this topic can be
found in [12], [9] and [16].
NP is unsettled, they can
still claim to be cryptographically secure in polynomial-time sense.
More details on this topic can be
found in [12], [9] and [16].



Next: Kolmogorov Complexity
Up: Randomness Assessments
Previous: -distributed
2001-05-30
![]() where
where ![]() is a prime and
is a prime and ![]() are integers greater than 1. For example,
are integers greater than 1. For example,
![]() because
because
![]() .
As long as the famous debate of P
.
As long as the famous debate of P![]() NP is unsettled, they can
still claim to be cryptographically secure in polynomial-time sense.
More details on this topic can be
found in [12], [9] and [16].
NP is unsettled, they can
still claim to be cryptographically secure in polynomial-time sense.
More details on this topic can be
found in [12], [9] and [16].