Citation: Rocha, Luis M. [1999]. "Evidence Sets: Modeling Subjective Categories" International Journal of General Systems. Vol. 27, pp. 457-494. Received 21 April 1995; In final form 27 June 1997.
This paper is available in Adobe Acrobat (.pdf) format or in postscript (zipped). Note that this paper contains many equations and figures. The HTML version may not display properly in all browsers; to get a version more true to the original I recommend the adobe pdf version.
Abstract: Zadeh's Fuzzy Sets are extended with the Dempster-Shafer Theory of Evidence into a new mathematical structure called Evidence Sets, which can capture more efficiently all recognized forms of uncertainty in a formalism that explicitly models the subjective context dependencies of linguistic categories. A belief-based theory of Approximate Reasoning is proposed for these structures. Evidence sets are then used in the development of a relational database architecture useful for the data mining of information stored in several networked databases. This useful data mining application establishes an Artificial Intelligence model of Cognitive Categorization with a hybrid architecture that possesses both connectionist and symbolic attributes.
INDEX TERMS: Fuzzy Sets, Dempster-Shafer Theory of Evidence, Interval Valued Fuzzy Sets, Uncertainty, Cognitive Categorization, Constructivism, Relational Databases, Distributed Memory, Information Technology; Information Retrieval; Adaptive Collaborative Systems; Knowledge Management.
Categories are bundles of concepts somehow associated in some context. Cognitive agents survive in a particular environment by categorizing their perceptions, feelings, thoughts, and language. The evolutionary value of categorization skills is related to the ability cognitive agents have to discriminate and group relevant events in their environments which may demand reactions necessary for their survival. If organisms can map a potentially infinite number of events in their environments to a relatively small number of categories of events demanding a particular reaction, and if this mapping allows them to respond effectively to relevant aspects of their environment, then only a finite amount of memory is necessary for an organism to respond to a potentially infinitely complex environment.
Thus, knowledge is equated with the survival of organisms capable of using memories of categorization processes to choose suitable actions in different environmental contexts. It is not the purpose here to dwell into the interesting issues of evolutionary epistemology [Campbell, 1974; Lorenz, 1971], I merely want to start this discussion by positioning categorization as a very important aspect of the survival of memory empowered organisms. Understanding categorization as an evolutionary (control) relationship between a memory empowered organism and its environment, implies the understanding of knowledge not as a completely observer independent mapping of real world categories into an organism's memory, but rather as the organism's, embodied, thus subjective, own construction of relevant - to its survival - distinctions in its environment. These ideas have been developed in more detail in [Rocha, 1997a, 1997b; Henry and Rocha, 1996] where an epistemological position named Evolutionary Constructivism is outlined and defended.
Since effective categorization of a potentially infinitely complex environment allows an organism to survive with limited amounts of memory, we can also see a connection between uncertainty and categorization. Klir [1991] has argued that the utilization of uncertainty is an important tool to tackle complexity. If the embodiment of an organism allows it to recognize (construct) relevant events in its environment, but if all the recognizable events are still too complex to grasp by a limited memory system, the establishment of one-to-many relations between tokens of these events and the events themselves, might be advantageous for its survival. In other words, the introduction of uncertainty may be a necessity for systems with a limited amount of memory, in order to maintain relevant information about their environments. Thus, it is considered important for models of human categories to capture all recognized forms of uncertainty. In the following, I address the historical relation between set theory and our understanding of categories; in particular, I discuss what kind of extensions we need to impose on fuzzy sets so that they may become better tools in the modeling of subjective, uncertain, cognitive categories.
It is important to separate the idea of a model of cognitive categorization and a model of a category. Though obviously dependent on one another, categories are included in more general models of cognitive categorization and knowledge representation. Agreeing on what the structure of a category might be, is far from agreeing on what the structure and workings of cognitive categorization models should be. It is also a simpler problem. Though, undoubtedly, the specific model of knowledge organization selected will dictate some of the properties of categories, the particular structure chosen to represent categories in such models does not have to offer an explanation for knowledge organization. All that is asked of a good category representation, is that it may allow the larger imbedding model of knowledge representation to function. For instance, if we use sets to represent categories, our models of knowledge representation may use set theory connectives and/or they may use more complicated sets of mappings or even introduce connectionist machines to produce the sets [Clark, 1993]. Thus, evaluating sets as prospective representations of categories should be done by analyzing the kinds of limitations they necessarily impose on any kind of model, and not simply models circumscribed to basic set-theoretic operations.
The classical theory of categorization defines categories as containers of elements with common properties. Naturally, the classic, crisp, set structure was ideal to represent such containers: an element of a universe of observation can be either inside or outside a certain category, if it has or has not, respectively, the defining properties of the category in question. Further, all elements have equal standing in the category: there are no preferred representatives of a category - all or nothing membership.
One other characteristic of the classical view of categorization has to do with an observer independent epistemology: realism or objectivism. Cognitive categories were thought to represent objective distinctions in the real world; say, divisions between colors, between sounds, were all assumed to be characteristics of the real world independent from any beings doing the categorizing. Frequently, this objectivism is linked to the way classical categories are constructed on all-or-nothing sets of objects: "if categories are defined only by properties inherent in the members, then categories should be independent of the peculiarities of any beings doing the categorizing" [Lakoff, 1987, page 7]. I do not subscribe to this point of view; we can use classical categories both in realist or constructivist epistemologies. Even with classical, all-or-nothing, categories, the properties are not inherent in the members, there is always something or someone defining the necessary list of properties. The question is who or what is to establish the shared properties of a particular category. A model where these shared properties are regarded as observer dependent, that is, established in reference to the particular physiology and cognition of the agent doing the categorizing, is built under a constructivist epistemology. If on the other hand, these properties are considered to be the ultimate truth of the real world, then the aim is the definition of an objectivist model of reality.
Most modern theories of categorization include classical categories as a special case of a more complex scheme, which does not imply that some categories are objective and others are subjective. Thus, classical categories have to do with an all-or-nothing description of sets, based on a list of shared properties defined in some model. This external model is indeed built within an objectivist epistemology in the classical approach, but these two aspects of the classical theory of categorization are not necessarily dependent. The chosen structure of categories and the chosen model of knowledge representation/manipulation, which can be realist or constructivist, may be independent concerns when modeling cognitive categorization.
Rosch [1975, 1978] proposed a theory of category prototypes in which, basically, some elements are considered better representatives of a category than others. It was also shown that most categories cannot be defined by a mere listing of properties shared by all elements. Some approaches define this degree of representativeness as the distance to a salient example element of the category: a prototype [Medin and Schaffer, 1978]. More recently, prototypes have been accepted as abstract entities, and not necessarily a real element of the category [Smith and Medin, 1981]. An example would be the categorization of eggs by Lorenz'[1981] geese, who seem to use an abstract prototype element based on such attributes as color, speckled pattern, shape, and size. It is easy to fool a goose with a wooden egg if the abstract characteristics of the prototype are emphasized.
Naturally, fuzzy sets became candidates for the simulation of prototype categories on two counts: (i) membership degrees could represent the degree of prototypicality of a concept regarding a particular category; (ii) a category could also be defined as the degree to which its elements observe a number of properties, in particular, these properties may represent relevant characteristics of the prototype. These two points are distinct. The first makes no claim whatsoever on the mechanisms of creation and manipulation of categories. It may be challenged, as I will do in the sequel, on the grounds that due to its simplicity, models using it must be extremely complicated. Nonetheless, it does offer the minimum requirement a category must observe: a group (set) of elements with varying degrees of representativeness of the category itself.
The second point goes beyond the definition of a category and enters the domain of modeling the creation of categories. As in the classic case, categories are seen as groups of elements observing a list of properties, the only difference is that elements are allowed to observe these properties to a degree. However, the so called radial categories [Lakoff, 1987] cannot be formed by a listing of properties shared by all its elements, even if to a degree. They refer to categories possessing a central subcategory core, defined by some coherent (to a model or context) listing of properties, plus some other elements which must be learned one by one once different contexts are introduced, but which are unpredictable from the core's context and its listing of shared properties. Thus, the second interpretation of fuzzy sets as categories leads fuzzy logic to a corner which renders it uninteresting to the modeling of cognitive categorization. Notice that Rosch herself made a distinction between the notion of category prototypes and the notion of knowledge representation:
"Prototypes do not constitute any particular processing model for categories [...]. What the facts about prototypicality do contribute to processing notions is a constraint -- process models should not be inconsistent with the known facts about prototypes. [...] As with processing models, the facts about prototypes can only constrain, but do not determine, models of representation." [Rosch, 1978, pg. 40]
Since fuzzy sets, at least to a degree, can be included in realist or constructivist frameworks, its dismissal as good models of cognitive categories has to be made on different grounds. In the following I will maintain that fuzzy sets are unsatisfactory because they (i) lead to very complicated models, (ii) do not capture all forms of uncertainty necessary to model mental behavior, and (iii) leave all the considerations of a logic of subjective belief to the larger imbedding model, which makes them poor tools in evolutionary constructivist approaches. A formal extension based on evidence theory is proposed next.
As Hampton [1992] and Clark [1993] discuss, the important question to ask at this point is "where do the prototypicality degrees come from?" Barsalou [1987] has shown how the prototypical judgments of categories are very unstable across contexts. He proposes that these judgements, and therefore the structure of categories, are constructed "on the hoof" from contextual subsets of information stored in long-term memory. The conclusion is that such a wide variety of context-adapting categories cannot be stored in our brains, they are instead dynamic categories which are rarely, if ever, constructed twice by the same cognitive system. Categories may indeed have Rosch's graded prototypicality structure, but they are not stored as such, merely constructed "on the hoof" from some other form of information storage system.
"Invariant representations of categories do not exist in human cognitive systems. Instead, invariant representations of categories are analytic fictions created by those who study them." [Barsalou, 1987 p. 114]
As Clark [1993] points out, since the evidence for graded categories is so strong, even in ad hoc categories such as "things that could fall on your head" or viewpoint-related categories, "it seems implausible to suppose that the gradations are built into some preexisting conceptual unit or prototype that has been simply extracted whole out of long-term memory." [Ibid, page 93] Thus, we should take the graded prototypical categories as representations of these highly transient, context-dependent knowledge arrangements, and not of models of information storage in the brain. In the following, the extensions of fuzzy sets proposed to model cognitive categories should be understood as such. As for the modeling of cognitive categorization itself, an attempt to model certain aspects of it is developed with the extended theory of approximate reasoning presented in section 7, which is used in a computational system of information retrieval outlined in section 9.
Let X denote a nonempty universal set under consideration. Let P(X) denote the power set of X. An element of X represents a possible value for a variable x. X can be countable or uncountable.
George Klir [1993; Klir and Yuan, 1995] classifies uncertainty into two main forms: ambiguity and fuzziness. Ambiguity is further divided into the categories of nonspecificity and conflict. Mathematically ambiguity is identified with the existence of one-to-many relations, that is, when several alternatives exist for the same question or proposition. Nonspecificity is associated with unspecified alternatives, and conflict with the existence of several alternatives with some distinctive characteristic. Dempster-Shafer Theory (see below) provides an ideal framework for the study of ambiguity, as it enlarges the scope of traditional probability theory. Fuzziness is identified with lack of sharp distinctions. Fuzzy sets (see below) are usually used to formalize this kind of uncertainty. A measure of fuzziness is defined as the lack of distinction between a set and its complement [Yager, 1979, 1980]. In [Rocha, 1997a, 1997b] measures of uncertainty needed to measure the information content of evidence sets presented next were developed. In particular, such measures were defined for both discrete and nondiscrete domains. Please refer to [Rocha, 1997a, 1997b] for a more detailed discussion of uncertainty.
Evidence theory, or Dempster-Shafer Theory (DST) [Shafer, 1976], may be defined in terms of a set function m: P (X) [0, 1], referred to as a basic probability assignment, such that m(emptyset)=0 and SUM m(A)=1. The value m(A) denotes the proportion of all available evidence which supports the claim that A in P (X) approximately represents the actual value of our variable x. DST is based on a pair of nonadditive measures: belief (Bel) and plausibility (Pl) uniquely obtained from m. Given a basic probability assignment m, Bel and Pl are determined for all A in P (X) by the equations:
the expressions above imply that belief and plausibility are dual measures related by:
for all A in P (X), where Ac represents the complement of A in X. It is also true that Bel(A) < Pl(A) for all A P (X). Notice that [Shafer, 1976, page 38] , "m(A) measures the belief one commits exactly to A, not the total belief that one commits to A." Bel(A), the total belief committed to A, is instead given by the sum of all the values of m for all subsets of A.
Any set A in P (X) with m(A) > 0 is called a focal element. A body of evidence is defined by the pair (F, m), where F represents the set of all focal elements in X, and m the associated basic probability assignment. The set of all bodies of evidence is denoted by B. In the context of evidence theory, the universal set X is referred to as the frame of discernment. Given two pairs of dual belief-plausibility measures, Bel1-Pl1, Bel2-Pl2, over the same of frame of discernment X, but based on different bodies of evidence (F, m)1, (F, m)2, the resulting, combined, body of evidence, (F, m)1,2, is defined by the following basic probability assignment:
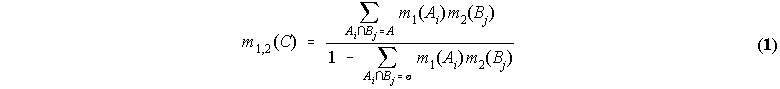
where F1,2 is the set of all non-empty subsets C of X resulting from the intersection of each focal element Ai of F1 with each focal element Bj of F2. This expression is referred to as the Dempster's rule of combination.
A crisp set entails no uncertainty in its membership assessment: if an element x of X is a member of a set A in X,
then it will not be a member of its complement Ac in X. A fuzzy set introduces fuzziness as the above law of
contradiction is violated: x can both be a member (to a degree) of A and Ac . A (standard) fuzzy set A is defined
by a membership function ![]() . Fuzzy sets can be extended to interval valued fuzzy sets (IVFS): A(x): X → I([0,1]), where I represents the set of intervals in [0, 1]. IVFS offer, in addition to fuzziness, a
nonspecific description of membership in a set; and they do so with very little information requirements. An
IVFS A, for each x in X, captures two forms of uncertainty: fuzziness (as in the case of fuzzy sets) and
nonspecificity. The Fuzziness of the membership degrees of standard fuzzy sets, is absolutely specific. When
we create a fuzzy set we have perfect knowledge of the degree to which a certain element x of X belongs to A.
In contrast, when we create an IVFS we have nonspecific knowledge of the degree of membership; hence the
utilization of an interval to describe the membership of x in A.
. Fuzzy sets can be extended to interval valued fuzzy sets (IVFS): A(x): X → I([0,1]), where I represents the set of intervals in [0, 1]. IVFS offer, in addition to fuzziness, a
nonspecific description of membership in a set; and they do so with very little information requirements. An
IVFS A, for each x in X, captures two forms of uncertainty: fuzziness (as in the case of fuzzy sets) and
nonspecificity. The Fuzziness of the membership degrees of standard fuzzy sets, is absolutely specific. When
we create a fuzzy set we have perfect knowledge of the degree to which a certain element x of X belongs to A.
In contrast, when we create an IVFS we have nonspecific knowledge of the degree of membership; hence the
utilization of an interval to describe the membership of x in A.
As previously discussed, fuzzy sets are actually fairly accurate representations of categories simply because they are able to represent prototypicality (understood as degree of representativeness); how the prototype degrees are constructed is, on the other hand, a different matter. Fuzzy sets are simple representations of categories which need much more complicated models of approximate reasoning than those fuzzy predicate logic alone can provide in order to satisfactorily model cognitive categorization processes. Critics [Osherson and Smith, 1981; Smith and Osherson, 1984; Lakoff, 1987] have shown that the several fuzzy set connectives (e.g. conjunction and disjunction) cannot conveniently account for the prototypicality of the elements of a complex category, which may depend only partially on the prototypicality of these elements in the constituent categories and may even be larger (or smaller) than in all of these. This is know as the prototype combination problem.
A complex category is assumed to be formed by the connection of several other categories. Approximate reasoning defines the sort of operations that can be used to instantiate this association. Smith and Osherson's [1984] results, showed that a single fuzzy connective cannot model the association of entire categories into more complex ones. Their analysis centered on the traditional fuzzy set connectives of (max-min) union and intersection. They observed that max-min rules cannot account for the membership degrees of elements of a complex category which may be lower than the minimum or higher than the maximum of their membership degrees in the constituent categories. Their analysis is very incomplete regarding the full-scope of fuzzy set connectives, since we can use other operators [see Dubois and Prade, 1985], to obtain any desired value of membership in the [0, 1] interval of membership. However, their basic criticism remains valid: even if we find an appropriate fuzzy set connective for a particular element, this connective will not yield an accurate value of membership for other elements of the same category. Hence, a model of cognitive categorization which uses fuzzy sets as categories will need several fuzzy set connectives to associate two categories into a more complex one (in the limit, one for each element). Such model will have to define the mechanisms which choose an appropriate connective for each element of a category. No single fuzzy set connective can account for the exceptions of different contexts, thus the necessity of a complex model which recognizes these several contexts before applying a particular connective to a particular element. Therefore, a model of cognitive categorization based solely on fuzzy sets and their connectives will be very complicated and cumbersome.
The prototype combination problem is not only a problem for fuzzy set models, but for all models of combination of prototype-based categories. Fodor [1981] insists that though it is true that prototype effects obviously occur in human cognitive processes, such structures cannot be fundamental for complex cognitive processes (high level associations): "there may, for example, be prototypical cities (London, Athens, Rome, New York); there may even be prototypical American Cities (New York, Chicago, Los Angeles); but there are surely not prototypical American cities situated on the east coast just a little south of Tennessee."[Ibid, page 297] As Clark [1993] points out, the problem with Fodor's point of view, and indeed the reason why fuzzy set combination of categories fails, is that "he assumes that prototype combination, if it is to occur, must consist in the linear addition of the properties of each contributing prototype." [Ibid, page 107] Clark proposes the use of connectionist prototype extraction as an easy way out of this problem. In fact, a neural network trained to recognize certain prototype patterns, e.g. some representation of "tea" and "soft drink", which is also able to represent a more complex category such as "ice tea", "does not do so by simply combining properties of the two 'constituent' prototypes. Instead, the webs of knowledge structure associated with each 'hot spot' engage in a delicate process of mutual activation and inhibition." [Ibid, page 107] In other words, complex categories are formed by nonlinear, emergent, prototype combination.
As Clark points out, however, this ability to nonlinearly combine prototypes in connectionist machines is a result of the pre-existence of a (loosely speaking) semantic metric which relates all knowledge stored in the network. Through the workings of the network with its inhibition and activation signals, new concepts can be learned which must somehow relate to the existing knowledge previously stored. Therefore, any new knowledge that a connectionist device gains, must be somehow related to previous knowledge. This dependence prevents the sort of open-ended conceptual combination that we require of higher cognitive processes.
This problem might be rephrased by saying that connectionist devices can only make nonlinear prototype combinations given a small number of contexts. The brain may use a network to classify, say, sounds, another one images, and so forth. In their own contexts, each network combines prototypes into more complex ones, but they cannot escape their own contexts. I believe, with Clark, that connectionist machines are nonetheless very powerful, even given these constraints. The approach I am about to follow, is not proposed to be used instead of connectionist devices, but one that may offer a higher level treatment of the contextual problem in prototype combination. In fact, in section 9, a computational model is presented that even though not using connectionist machines in the strong sense [van Gelder, 1992], uses networked relational databases that also possess distributed semantic semi-metrics and which can approach this contextual problem.
As discussed in the previous section, approximate reasoning does not model effectively the combination of prototypical categories. It can only work on very limited contexts, whose categories can be formed from the linear combination of constituent categories. The Introduction of a theory of approximate reasoning based on interval valued fuzzy sets [Gorzaczany, 1987; Türken, 1986] represents a step forward in the modeling of cognitive categorization, as it offers a second level of uncertainty, but it only slightly improves the contextual problem referred above. The membership degrees of IVFS are nonspecific (see section 3.3). This second dimension of uncertainty allows us to interpret the interval of membership of an element in a category as the membership degree of this element according to several different contexts, which we cannot a priori identify.
In particular, Turksen's concept combination mechanisms are based on the separation of the disjunctive and
conjunctive normal forms of logic compositions in fuzzy logic. A disjunctive normal form (DNF) is formed
with the disjunction of some of the four primary conjunctions, and the conjunctive normal form (CNF) is
formed with the conjunction of some of the four primary disjunctions, respectively:
![]() . In two-valued logic the CNF and DNF of a logic composition are equivalent: CNF = DNF. Turksen observed that in fuzzy logic, for certain families of conjugate
pairs of conjunctions and disjunctions, we have instead DNF ⊆ CNF for some of the fuzzy logic connectives.
He then proposed that fuzzy logic compositions could be represented by IVFS's given by the interval [DNF,
CNF] of the fuzzy set connective chosen [Turksen, 1986]. With IVFS based connectives, Turksen was able
to deal more effectively with the shortcomings of a pure fuzzy set approach. In his model, two fuzzy sets are
combined into an IVFS. The fuzzy and nonspecific degrees of membership of the elements in the category
obtained, can be interpreted as inclusion in a category according to several possible, fuzzy degrees.
. In two-valued logic the CNF and DNF of a logic composition are equivalent: CNF = DNF. Turksen observed that in fuzzy logic, for certain families of conjugate
pairs of conjunctions and disjunctions, we have instead DNF ⊆ CNF for some of the fuzzy logic connectives.
He then proposed that fuzzy logic compositions could be represented by IVFS's given by the interval [DNF,
CNF] of the fuzzy set connective chosen [Turksen, 1986]. With IVFS based connectives, Turksen was able
to deal more effectively with the shortcomings of a pure fuzzy set approach. In his model, two fuzzy sets are
combined into an IVFS. The fuzzy and nonspecific degrees of membership of the elements in the category
obtained, can be interpreted as inclusion in a category according to several possible, fuzzy degrees.
Turksen's model simplifies the pure fuzzy set approach since we will find more categories which can be combined into complex categories with a single connective used for all elements of the universal. The IVFS approach provides a way to acknowledge the existence of contextual nonspecificity in complex category formation, thus producing a more accurate representation of different forms of uncertainty present in such processes. The problem is that categories demand membership values which more than nonspecific can be conflicting. That is, the contextual effects may need more than an interval of variance to be accurately represented. Also, even though IVFS use nonspecific membership, thus allowing a certain amount of contextual variance, the several contexts are not explicitly accounted for in the categorical representation. Section 5 proposes set structures which (i) capture all recognizable forms of uncertainty in their membership representation, (ii) point explicitly to the contexts responsible for a certain facet of their membership representation, and (iii) in so doing, introduce a formalization of belief.
An alternative way to represent an IVFS A is to consider that for every element x of X, there is a body of
evidence (F x, mx) defined on the set of all intervals of [0,1], I, with a single focal element given by the interval
![]() . The basic probability assignment function mx assumes the value 1 for this single focal
element, representing our belief that the degree of membership of element x of X in A is (with all certainty) in
the sub-interval Ix of [0, 1]. In other words, our judgement of the (nonspecific) degree of membership, Ix, of
x in set A indicates that we fully believe it is correct. Notice that the universal set of the IVFS is X, but the
universal set of the body of evidence is the unit interval [0, 1]. It is now clear that an IVFS is a very special
case of a more general structure which I refer to as evidence set [Rocha, 1994, 1995, 1997a]. An evidence set
A of X, is defined by a membership function of the form:
. The basic probability assignment function mx assumes the value 1 for this single focal
element, representing our belief that the degree of membership of element x of X in A is (with all certainty) in
the sub-interval Ix of [0, 1]. In other words, our judgement of the (nonspecific) degree of membership, Ix, of
x in set A indicates that we fully believe it is correct. Notice that the universal set of the IVFS is X, but the
universal set of the body of evidence is the unit interval [0, 1]. It is now clear that an IVFS is a very special
case of a more general structure which I refer to as evidence set [Rocha, 1994, 1995, 1997a]. An evidence set
A of X, is defined by a membership function of the form:
A(x): X → B[0, 1]
where, B[0, 1] is the set of all possible bodies of evidence (F x, mx) on I. Such bodies of evidence are defined by a basic probability assignment mx on I, for every x in X. Thus, evidence sets are set structures which provide interval degrees of membership, weighted by the probability constraint of DST. They are defined by two complementary dimensions: membership and belief. The first represents a fuzzy, nonspecific, degree of membership, and the second a subjective degree of belief on that membership, which introduces conflict of evidence as several, subjectively defined, competing membership intervals weighted by the basic probability constraint are created (focal intervals). Figure 1 depicts a non-consonant [Rocha, 1995] evidence set with three focal elements.
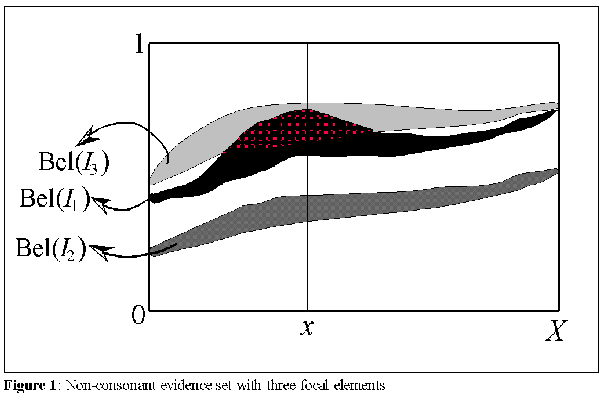
The interpretation I suggest for the multiple intervals of evidence sets, defines each interval of membership Ijx, with its correspondent evidential weight mx( Ijx), as the representation of the prototypicality of a particular element x of X in category A according to a particular perspective. Thus, each element x of an evidence set A has its membership defined as several intervals representing different, possibly conflicting, perspectives. An IVFS refers to the case where we have a single perspective on the category in question, even if it admits a nonspecific representation (an interval). The ability to maintain several of these perspectives, which may conflict at times allows a model of cognitive categorization or knowledge representation to directly access particular contexts affecting the definition of a particular category, which is essential for radial categories. In other words, the several intervals of membership of evidence sets refer to different perspectives which explicitly point to particular contexts.
The degrees of belief on which evidence theory is based do not aspire to be objective claims about some real evidence, they are rather proposed as judgements, formalized in the form of a degree [Shafer, 1976, page 21]. Likewise, Rosch's prototypes are not assumed to be an objective grading of concepts in a category, but rather judgements of some uncertain, highly context-dependent, grading [Rosch, 1978, page 40]. Evidence sets offer a way to model these ideas since an independent(1), unconstrained, membership grading of elements (concepts) in a category is offered together with an explicit formalization of the belief posited on this membership. For evidence sets, membership in a category and judgments over membership are different, complementary, qualities of prototypicality. None of the other structures so far presented is able to offer both an independent characterization of membership and a formalization of judgments imposed on this membership. Traditional set structures (crisp, fuzzy, or interval-valued) alone offer only an independent degree of membership, while evidence theory by itself offers primordially a formalization of belief which constrains the elements of a universal set with a probability restriction (more on this in section 8).
Regarding the previously discussed connectionist extraction of prototypes, notice that evidence sets, as any set structure, have independent, unconstrained membership. Connectionist prototypes are implicitly defined by a semantic metric constraining the elements of the categorizing universe. The existence of such metrics may be very important for cognitive categorization. However, evidence sets are merely proposed as models of cognitive categories, it is up to the model of cognitive categorization to supply additional constraints such as semantic metrics. As a higher level structure, it is very important that Evidence Sets do not have such constraints a priori, in fact, it is precisely their advantage over connectionist devices which are not flexible enough to allow users to arbitrarily change constraints and contexts on prototype-based categories. In section 7, approximate reasoning methods are proposed which shall be used in Section 9 to define an information retrieval system that in turn constrains Evidence Sets with context-specific semantic metrics.
A fuzzy set captures fuzziness in a specific way; an IVFS introduces nonspecificity; a consonant evidence set (nested focal intevals) introduces grades or shades of nonspecificity; and finally, a nonconsonant evidence set introduces conflict as we have cases where the degree to which an element is a member of a set is represented by disjoint focal intervals of [0, 1] with different evidential strengths. The three forms of uncertainty are clearly present in human cognitive processes. More than simply measuring fuzziness, as approximate reasoning models do, models of uncertain reasoning based on evidence sets need to effectively measure all the three uncertainty forms. Hence, we need a 3-tuple of measures of the 3 main kinds of uncertainty to aid us in the decision making steps of our uncertain reasoning models: (Fuzziness, Nonspecificity, Conflict). [Rocha et al, 1996; Rocha, 1997a, 1997b].
The three forms of uncertainty define a 3 dimensional uncertainty space for set structures, where crisp sets
occupy the origin, fuzzy sets the fuzziness axis, IVFS the fuzziness-nonspecificity plane, and evidence sets
most of the rest of this space. The total uncertainty, U, of an evidence set A is defined by:
![]() . The three indices of uncertainty, which vary between 1 and 0, IF (fuzziness), IN
(nonspecificity), and IS (conflict) were introduced in [Rocha, 1996a, 1997a, 1997b], where it was also proven
that IN and IS possess good axiomatic properties wanted of information measures. For a complete discussion,
please refer to [Rocha et al, 1996; Rocha, 1997a, 1997b].
. The three indices of uncertainty, which vary between 1 and 0, IF (fuzziness), IN
(nonspecificity), and IS (conflict) were introduced in [Rocha, 1996a, 1997a, 1997b], where it was also proven
that IN and IS possess good axiomatic properties wanted of information measures. For a complete discussion,
please refer to [Rocha et al, 1996; Rocha, 1997a, 1997b].
The operations of complementation, intersection, and union are the most basic connectives in a theory of approximate reasoning. Here I discuss only these operators, since all other connectives can be easily constructed from these. Naturally, complementation, intersection, and union as defined below for evidence sets subsume, as special cases, the same operations for IVFS and fuzzy sets.
The interval valued membership function of elements of X in an IVFS A is given by:
A(x) = ![]() . Its complement can be defined as the negation of the interval limits in reverse
order:
. Its complement can be defined as the negation of the interval limits in reverse
order: ![]() [Gorzaczany, 1987]. The membership function of an evidence set A
of X is given, for each x, by n intervals weighted by a basic probability assignment mx:
[Gorzaczany, 1987]. The membership function of an evidence set A
of X is given, for each x, by n intervals weighted by a basic probability assignment mx:
The complement of an evidence set [Rocha, 1997a, 1997c] is defined as the complement of each of its interval focal elements with the preservation of their respective evidential strengths:
The intersection of two IVFS [Gorzaczany, 1987] is defined as the minimum of their respective lower and
upper bounds of their membership intervals. Given two intervals of [0, 1] ![]() and
and
![]() , the minimum of both intervals is an interval
, the minimum of both intervals is an interval ![]() . Given
two evidence sets A and B defined for each x of X by:
. Given
two evidence sets A and B defined for each x of X by:
and
where Ii and Jj are intervals of [0,1]. Their intersection is an evidence set C(x) = A(x) B(x), whose intervals of membership Kk and respective basic probability assignment mC(Kk) are defined by:
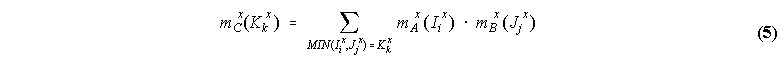
The union of two IVFS [Gorzaczany, 1987] is defined as the maximum of their respective lower and upper
bounds of their membership intervals. Given two intervals of [0, 1] ![]() and
and ![]() ,
the maximum of both intervals is an interval
,
the maximum of both intervals is an interval ![]() . Given two
evidence sets A and B defined by (3) and (4), their union is an evidence set C(x) = A(x) B(x), whose intervals
of membership Kk and respective basic probability assignment mC(Kk) are defined by:
. Given two
evidence sets A and B defined by (3) and (4), their union is an evidence set C(x) = A(x) B(x), whose intervals
of membership Kk and respective basic probability assignment mC(Kk) are defined by:
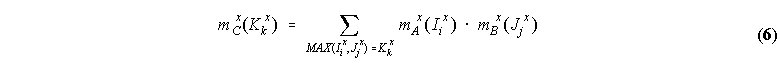
By utilizing the connectives (5) and (6), the uncertainty of our models tends to increase, as two bodies of evidence on the unit interval are combined into a new one, by preserving most perspectives (contexts) involved. There are at least as many intervals in the combined set as the minimum of intervals in the combining sets. In other words, if ix and jx represent the number of intervals (perspectives) present, respectively, in combining sets A and B for element x, then the combined set C will have at least MIN( | ix | , | jx | ) intervals for concept x. An alternative to this way of combining evidence sets is described below.
We can combine evidence sets by preserving all their perspectives (though with reduced weights as the joined basic assignment must still add up to 1) as above, thus increasing the uncertainty complexity, or we can combine them only according to the coherent perspectives (those aiming at the same intervals) by utilizing Dempster's rule of combination (1) presented in section 3.2 , and decrease the uncertainty complexity. Given two evidence sets A and B defined by (3) and (4), their uncertainty decreasing combination is an evidence set C(x) = A(x) ⊗ B(x), whose intervals of membership Kk and respective basic probability assignment mC(Kk) are defined by:
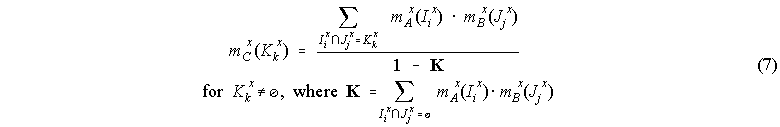
This operation eliminates all focal elements which do not coincide (or intersect) in both bodies of evidence being combined, while the operations of section 7.1 maintain some evidential weight for these, though enhancing those that do intersect.
Dempster's rule of combination is used to combine different bodies of evidence over the same frame of discernment. It is an all or nothing rule, that is, if the focal elements of two distinct bodies of evidence being combined are disjoint, no combination is possible. In this situation, in DST, if we still consider that there is relevant interaction between the two bodies of evidence which our frame of discernment cannot capture, then we either rethink our basic probability assignments or the frame of discernment is changed by introducing new elements common to both bodies of evidence. Now consider that our model of categorization, by utilizing Dempster's rule, reaches a combination of categories whose bodies of evidence are completely incoherent. That is, no new category is obtainable. If this result is reached in some intermediate step of an approximate reasoning process, the process is naturally stopped. To be able to continue with this process, we have to obtain some transitional category. Since the frame of discernment of the belief attributes of an evidence set is the membership unit interval, we cannot aim to refine it in any way. For this reason, I have proposed uncertainty decreasing and increasing operations for evidence sets. If the evidence sets being combined are at least partially coherent, we can use Dempster's rule which will reduce the uncertainty present. If this coherency is not attainable, we can choose an uncertainty increasing operation which largely maintains the evidence from both structures being combined, until a more coherent state of evidence is encountered at a later stage.
The uncertainty decreasing operation can be used when we have coherent evidence of membership in combining evidence sets, and when we wish to reduce dramatically the amount of uncertainty present in some simulation of human reasoning processes. In an artificial system, this operation might be identified we fast decision-making processes. Say, if we possess two categories which must be combined in order to make a fast decision, then uncertainty must be reduced and the most coherent result chosen. On the other hand, if we do not have coherent membership evidence, or if we do not need to engage in fast decision making, but instead desire to search for more conflicting, far-fetched, associations (from wildly different contexts), then the uncertainty increasing operations should be chosen.
So far I have discussed set structures as models of cognitive categories, from crisp sets to evidence sets I have stressed that any mathematical model of cognitive categories must offer (i) degrees of inclusion in the category/set, (ii) an accurate account of uncertainty forms in their membership values, and (iii) a way in for context-dependencies and subjective aspects of categories. I have proposed that evidence sets fulfill these three requirements. A natural question now is, why is DST not enough by itself to effectively model cognitive categories? We can think of the frame of discernment of DST as the universe of possible values for a variable x representing the possible elements (or concepts) of a universe of discourse. A category can be defined as a body of evidence defined on such universe. Each focal element, can be seen as a possible perspective for the category.
Let us consider that a category is defined by a body of evidence (F, m) on a universal set X. In other words, the category will be defined by a set F of subsets of X (focal elements) with associated basic probability assignment m. Plausibility and belief measures can be constructed from (F, m) as defined in section 3.2. Following Dempster's [1967] original interpretation of plausibility and belief measures as upper and lower probabilities, respectively, we can understand these probability limits as offering a nonspecific (interval-valued) membership of subsets of X in the category, which would satisfy the first requirement above. Nonetheless, several problems are encountered with this model of categories. First, notice that the basic probability assignment values must add up to one (see section 3.2), this constrains the category as it introduces a dependency on its elements. That is, because of the probabilistic constraint, the value of membership of an element, which would be given here by the belief-plausibility interval, would be constrained by the value of membership of other elements. Specifically, their individual membership is not free to attain any value as it is desired of a set structure or a cognitive category. Furthermore, membership in a category is not attributed to singletons but to subsets of the universal set. In addition, the second and third requirements are not satisfied as conflict is not captured, and no account of context is included, in the individual membership values.
Consider now that a category is still defined by the body of evidence (F, m), only now, more in line with Shafer's [1976] interpretation, the basic probability assignment function m will identify the portions of belief ascribed exactly to the focal elements F. This way, each exact portion of belief and its associated focal element can be related to a particular context in a larger imbedding model. In other words, the sort of categories we obtain with this interpretation are formed by crisp subsets of the frame of discernment with associated belief values: membership is all or nothing, but belief is graded. In a way, we have classic categories with an account of belief, subjectivity, and a way in for context-dependencies in a larger model of categorization. Clearly, this interpretation satisfies the third requirement but not the first and the second.
Several ways of extending the DST to a fuzzy set framework have been proposed. Probably the most general and well known approach is John Yen's [1990] generalization. Basically, the idea is to move from crisp to fuzzy focal elements. In this case, we no longer have classical categories, as degrees of membership are introduced, thus satisfying the first requirement in addition to the third requirement already satisfied by the second interpretation of evidence theory in the previous section. Naturally, to satisfy the second requirement, that is, to obtain an accurate account of uncertainty forms in the membership degrees of a set/category's elements we can extend the fuzzy focal elements to interval-valued focal elements, or even more generally to sets of fuzzy sets. This seems to satisfy all of the three requirements above, so, why are evidence sets preferable over generalized evidence theory as models of categories? The next subsection should answer this question.
Evidence sets have unconstrained membership; that is, the values of membership for each element x of the universal set X are independent of each other. In contrast, the categories defined solely with evidence theory in the previous sections, are set oriented, that is, they define categories with focal elements which are subsets of X. Thus, the evidence a particular context offers is associated with a set of singletons rather than with a singleton itself. Naturally, a singleton can also be represented by a set, but if focal elements are singletons, then we will need many focal elements to represent a category, and since their respective evidential weights given by the basic probability assignment must add up to one, each singleton will necessarily have a small degree of belief associated with it. In other words, the belief we have that a certain singleton belongs to a category, will be dependent on the belief we ascribe to other singletons. This kind of dependence is not desirable of a model of a category. The inclusion of an element in a category should not necessarily be dependent on other elements already included in it. A larger model of categorization may impose these constraints at a higher level, but the basic mathematical structures used should not impose them at the onset.
An evidence set allows a complete separation of membership and belief between elements in a category since an account of belief is not used to constrain the elements of the universal set but to constrain their respective membership values in the unit interval. Thus, the membership/belief of an element x is independent from that of another element y. It is important to realize that belief is still constrained for each individual membership qualification, in other words, the basic probability assignment used to qualify the possible intervals of membership, must still add up to one. With this independent quantifiability of membership/belief for each element in a universal set, the contexts that affect an element's membership in a category can be completely different from element to element, a desirable characteristic for radial categories.
In this section a conversational, collaborative, adaptive, knowledge management system for databases that uses evidence sets as categorization mechanisms is presented. Its objective is the definition of a human-machine interface that can capture more efficiently the user's interests through an interactive question-answering process. It also attempts to model certain aspects of cognitive categorization processes that use linguistic categories as higher-level short-term constructs generated by lower-level connectionist memory banks. The model offers an expansion of Nakamura and Iwai's [1982] data-retrieval system which is expanded from a fuzzy set to an evidence set framework. The evidence set expansion allows the construction of categories from several databases simultaneously.
Each database is characterized by a network structure with two different kinds of objects: Concepts xi (e.g. Keywords) and Properties pi (e.g. data records like books). Each concept is associated with a number of properties which may be shared with other concepts. Based on the amount of properties shared with one another, a measure of similarity, s, can be constructed for concepts xi and xj:
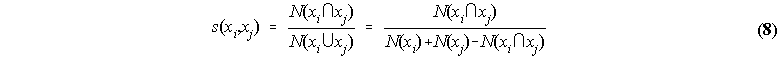
where N(xi) represents the number of properties that directly qualify concept xi, N(xi) represents the number of properties that directly qualify concept xi, N(xi ∪ xj) represents the number of properties that directly qualify both xi or xj, and N(xi ∩ xj) represents the number of properties that directly qualify either xi or xj. The inverse of the similarity, s, creates a measure of distance(2), d:
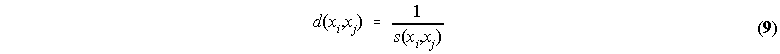
The distances between directly linked concepts are calculated using (9). After this, the shortest path is calculated between indirectly linked concepts. The algorithm allows the search of indirect distances up to a certain level. The set of n-reachable concepts from concept xi, is the set of concepts that have no more that n direct paths between them. If we set the algorithm to paths up to level n, all concepts that are only reachable in more than n direct paths from xi will have their distance to xi set to infinity.
The Local Knowledge Context Xk is the substructure of database k defined solely by the concepts and their relative distance dk as constructed with the semi-metric (9). Its purpose is to capture human knowledge by keeping a record of relationships between concepts, as well as a measure of their similarity. It is not a connectionist structure in the strong sense that concepts are not superposed [van Gelder, 1992] over the network but localized in recognizable nodes. However, in addition to localized nodes it does possess a distributed semi-metric space relating all knowledge as desired of connectionist memory [Clark, 1993]. This space is the lower-level structure of the system, the long-term memory of the database. It is from this semantic semi-metric that temporary prototype categorizations can be formed to model the "on the hoof" categories previously discussed.
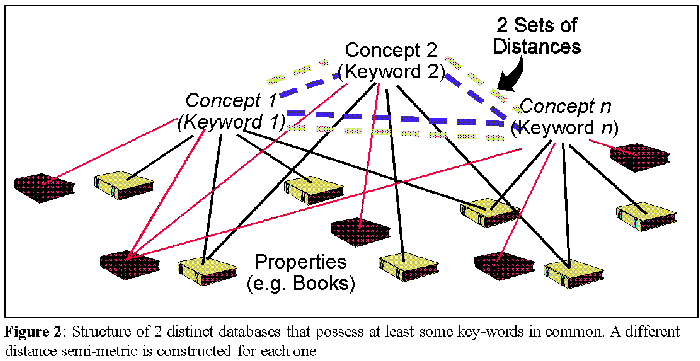
The system's relations are unique to it, and reflect the actual semantic constraints established by the set of properties (data records) it stores. Thus, the semantic semi-metric defined by (9), reflects the actual inter-significance of concepts (keywords) for the system and its users. The same concept in different databases will be related differently to other concepts, because the actual properties stored will be distinct. The properties a database stores are a result of its history of utilization and deployment of information by its users. In this sense, the long-term networked memory structure reflects a unique subjectivity developed by the history and dynamics of information storage and usage. Thus, each local knowledge space Xk from database k captures the knowledge that its community of users have accumulated in some area. Figure 2 depicts such structure with two different relational databases.
The Total Knowledge Space X of this structure is the set of all concepts in the nd included databases, that is:
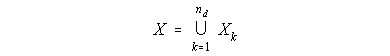
Furthermore, the system has nd different distance semi-metrics, dk, associated with it. Each distance semi-metric is still built with equation (9) for some acceptable level of n-reachable concepts. But since each of the nd databases has a different concept-property pattern of connectivity, each distance semi-metric dk will be different. When a concept exists in one database and not on another, its distance to all other concepts of the second database is set to infinity. If the databases reflect similar communities of users, naturally their distance semi-metrics will tend to be more similar. This distinction between the several local knowledge contexts provides the system with intrinsic contextual conflict in evidence.
With their several intervals of membership weighted by the basic probability assignment of DST, evidence sets can be used to quantify the relative interest of users in each of the knowledge contexts stored in the nd databases. Given the underlying relations imbedded in the knowledge space, the system uses a question-answering process to capture the interests of users in terms of this relational structure. In other words, the system constructs its own internal categories in interaction with the community of users. The extended evidence set approximate reasoning operations of intersection and union can be used to define such a conversational process.
The system starts by presenting users with the several networked databases available, who have to probabilistically grade them. That is, weights must be assigned to each database which must add to one (in order to build basic probability assignment functions). The selected databases define the several contexts which the system uses to construct its categories. Once this is defined, the question-answering algorithm is as follows:
Several approaches can be used to define evidence set membership functions for the algorithm above. The scheme I follow here starts by building bell-shaped fuzzy membership functions for each of the nd distance semi-metrics dk of X [Nakamura and Iwai, 1982]. Thus we obtain nd different fuzzy subsets of X defined by fuzzy membership functions for "YES" or "NO" responses given to concept xi as follows:
and
where the parameter controls the spread of the bell-shaped functions.
The next step is the construction of IVFS from these nd fuzzy sets, using Turksen's DNF ⊆ CNF combinations
(see section 4.2). All pairs of the nd fuzzy sets given by either (10) or (11) for the "YES" or "NO" case
respectively are combined to obtain ![]() IVFS for the union combination and
IVFS for the union combination and ![]() for the
intersection combination. Each pair of fuzzy sets is combined with the CNF and DNF forms of disjunction
(union) and conjunction (intersection) in order to form two IVFS whose respective intervals of membership are
defined by the DNF ⊆ CNF bounds for the standard union and intersection. Thus, from nd fuzzy sets we obtain
for the
intersection combination. Each pair of fuzzy sets is combined with the CNF and DNF forms of disjunction
(union) and conjunction (intersection) in order to form two IVFS whose respective intervals of membership are
defined by the DNF ⊆ CNF bounds for the standard union and intersection. Thus, from nd fuzzy sets we obtain
![]() IVFS. Since the "YES" and "NO" functions are combined in exactly the same way, in the following
I define the IVFS combination for a series of nd fuzzy set membership functions that can refer to either "YES"
or "NO". Formally, a pair of fuzzy set membership functions (for semi-metrics dk and dl) is combined to obtain
two IVFS:
IVFS. Since the "YES" and "NO" functions are combined in exactly the same way, in the following
I define the IVFS combination for a series of nd fuzzy set membership functions that can refer to either "YES"
or "NO". Formally, a pair of fuzzy set membership functions (for semi-metrics dk and dl) is combined to obtain
two IVFS:
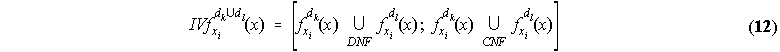
for union, and
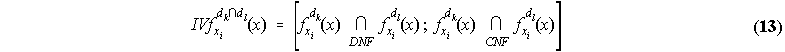
for intersection, where for two fuzzy sets A(x), B(x) the following definitions apply (the over line denotes set complement):
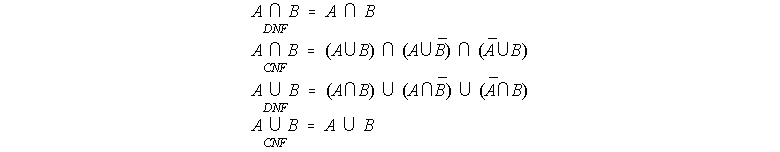
The final step is the construction of an evidence set from the ![]() IVFS obtained from (12) and (13). At the
onset, the user specifies the relative weight of the nd databases utilized, mk, which form a probability restriction
since the sum of all mk for k=1...nd must equal one. When two fuzzy sets
IVFS obtained from (12) and (13). At the
onset, the user specifies the relative weight of the nd databases utilized, mk, which form a probability restriction
since the sum of all mk for k=1...nd must equal one. When two fuzzy sets ![]() and
and ![]() , with relative
weights mk and ml respectively, are combined with (12) and (13) to obtain two IVFS, the total weight ascribed
to this pair of IVFS is (mk + ml)/(nd - 1), and half of this quantity to each IVFS, which guarantees that the
several IVFS are weighted by a probability restriction. Thus, if we have nd databases, with probability weight
mk (k=1...nd), the evidence set membership function for an answer "YES" to concept xi of knowledge space X,
is given by:
, with relative
weights mk and ml respectively, are combined with (12) and (13) to obtain two IVFS, the total weight ascribed
to this pair of IVFS is (mk + ml)/(nd - 1), and half of this quantity to each IVFS, which guarantees that the
several IVFS are weighted by a probability restriction. Thus, if we have nd databases, with probability weight
mk (k=1...nd), the evidence set membership function for an answer "YES" to concept xi of knowledge space X,
is given by:
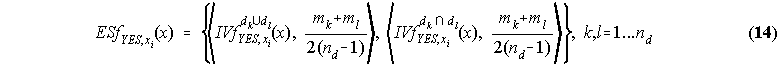
that is, the evidence set has ![]() focal intervals constructed from (12) and (13), weighted as described
above. When several focal intervals coincide, their weights are summed and only one interval is acknowledged.
The procedure for the "NO" evidence set is equivalent. Figure 3 depicts the construction of the "YES" evidence
set membership function for a case of nd=2.
focal intervals constructed from (12) and (13), weighted as described
above. When several focal intervals coincide, their weights are summed and only one interval is acknowledged.
The procedure for the "NO" evidence set is equivalent. Figure 3 depicts the construction of the "YES" evidence
set membership function for a case of nd=2.
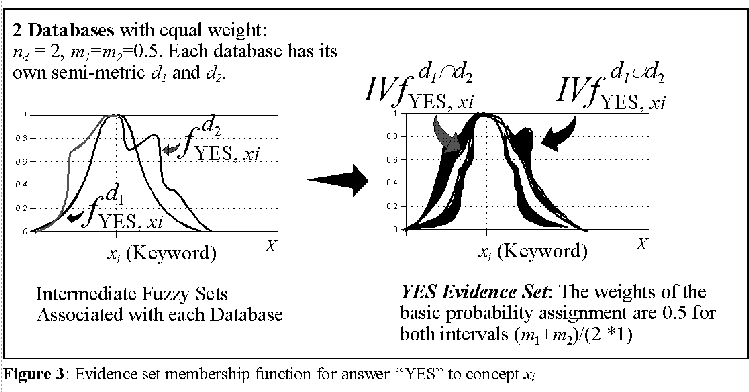
The two different semi-metrics d1 and d2 for the knowledge space X cause the category constructed for the "YES" answer to concept xi to be more than just fuzzy, also nonspecific and conflicting. It is important to stress that this more accurate construction of prototypical categories includes more uncertainty forms as a result of structural differences in the information stored in the several distributed memory contexts utilized. It is the lower level conflicts of long-term memory that the short-term construction of categories tailored by users reflects. This algorithm, implements many of the, temporary, "on the hoof" [Clark, 1993] category constructions ideas as discussed previously. In particular, it is based on a long-term memory bank of semantic relations that reflects the conceptual relationships of the community of users. Prototype categories are then built using evidence sets which reflect such consensually built relational metrics and the directed interest of a particular user at a particular time.
After construction of the learned category A(x), the system must return to the user the properties (data records
such as books) relevant to this category. Notice that every property pi defines a crisp subset of the total
knowledge space X whose elements are all the concepts to which pi is directly connected in any of the
constituent databases. Let this subset be represented by ![]() . Since each property defines a crisp subset of
X, the similarity between this crisp subset and the evidence subset defined by the learned category is a measure
of the relevance of the property to the learned category. One way to define this measure of similarity is to
approximate the evidence set category to its closest fuzzy set by a process of elimination of nonspecificity and
conflict. Once this fuzzy set is obtained the following measures of similarity between properties and learned
categories can be defined:
. Since each property defines a crisp subset of
X, the similarity between this crisp subset and the evidence subset defined by the learned category is a measure
of the relevance of the property to the learned category. One way to define this measure of similarity is to
approximate the evidence set category to its closest fuzzy set by a process of elimination of nonspecificity and
conflict. Once this fuzzy set is obtained the following measures of similarity between properties and learned
categories can be defined:
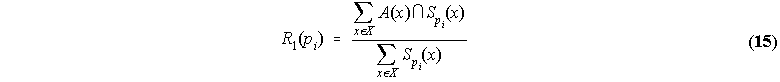
and
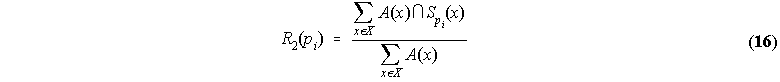
R1 yields the fuzzy cardinality of the fuzzy set given by the intersection of the learned category A(x) with
![]() over the cardinality of the latter: it is an index of the subsethood of
over the cardinality of the latter: it is an index of the subsethood of ![]() in A(x). The more
in A(x). The more ![]() is a
subset of A(x), the more relevant pi is. As long as
is a
subset of A(x), the more relevant pi is. As long as ![]() is included to a large extent in A, the property pi will
be considered very relevant, even if the learned category contains many more concepts than those included in
is included to a large extent in A, the property pi will
be considered very relevant, even if the learned category contains many more concepts than those included in
![]() . This way, R1 gives high marks to all those properties who form subsets of the learned category and not
necessarily those properties that qualify (are related to) the entire learned category as a whole. It is an index
that emphasizes the independence of the concepts of the learned category. It should be used when the cardinality
of A(x) is large, otherwise, very few properties will exist that qualify such large set of concepts.
. This way, R1 gives high marks to all those properties who form subsets of the learned category and not
necessarily those properties that qualify (are related to) the entire learned category as a whole. It is an index
that emphasizes the independence of the concepts of the learned category. It should be used when the cardinality
of A(x) is large, otherwise, very few properties will exist that qualify such large set of concepts.
R2, on the other hand, yields the fuzzy cardinality of the fuzzy set given by the intersection of the learned
category A(x) with ![]() over the cardinality of the former: it is an index of the subsethood of A(x) in
over the cardinality of the former: it is an index of the subsethood of A(x) in ![]() .
The more A(x) is a subset of
.
The more A(x) is a subset of ![]() , the more relevant pi is. This way, R2 gives high marks to all those properties
who form subsets that include the learned category as a whole. It is an index that emphasizes the dependence
of the concepts of the learned category. It should be used when the cardinality of A(x) is small.
, the more relevant pi is. This way, R2 gives high marks to all those properties
who form subsets that include the learned category as a whole. It is an index that emphasizes the dependence
of the concepts of the learned category. It should be used when the cardinality of A(x) is small.
Thus, after the system finishes its construction of the learned category A(x), the user can select one of the indices given by (15), (16), or a combination of the two and a value between 0 and 1. High values will result on the system returning only those properties highly related to A(x) according to the index chosen. Lower values will result in many more items being included in the list of returned properties.
It is also desirable to provide this system with a mechanism to adapt the long-term relational structure, the knowledge space, according to the system's interactions with its users. Due to the properties (data records) it stores, the system may fail to construct strong relations between concepts (keywords) that its users find relevant. Therefore, the more certain concepts are associated with each other, by often being simultaneously included with a high degree of membership in learned categories, the more the distance between them should be reduced. An easy way to achieve this is to have the values of N(xi) and N(xi, xj) as defined in (8), adaptively altered for each of the constituent nd databases. After an evidence set learned category is constructed and reduced to a fuzzy set A(x), these values can be changed to:
and
respectively (t indicates the current state and t+1 the new state). This implements an adaption of the system to its users according to repeated interaction. Thus, the system though constructing its categories according to its own distributed long-term memory, will adapt its constructions as it engages in question-answering conversations with its users. The direction of this adaptation leads the system's relational structure to match more and more the expectations of the community of users with whom the system interacts. In other words, its constructions are consensually selected by the community of users. Furthermore, when two highly activated concepts in the learned category are not present in the same database (each one exists in a different database) they are added to the database which does not contain them, with property counts given by equations (17) and (18). If the simultaneous activation keeps occurring, then a database that did not previously contain a certain concept, will have its presence progressively strengthened, even though such concept does not really possess any properties in this database.
If we regard the system's learned categories, implemented as evidence sets, as linguistic prototypical categories, which are the basis of the system's communication with its users, then such categories are precisely a mechanism to achieve the structural perturbation of its long-term distributed memory in order to lead it to increasing adaptation to its environment. In addition, short-term memory not only adapts an existing structure to its users, but effectively creates new elements in different, otherwise independent, relational databases, solely by virtue of its temporary construction of categories This way, linguistic categories function as a system of consensual structural perturbation of distributed memory banks, capable of transferring information across different contexts. This pragmatic adaptation to an environment has been argued to function as a model of an evolving semiosis between cognitive systems and their environments which validates a position of Evolutionary Constructivism [Henry and Rocha, 1996; Rocha, 1997a, 1997b].
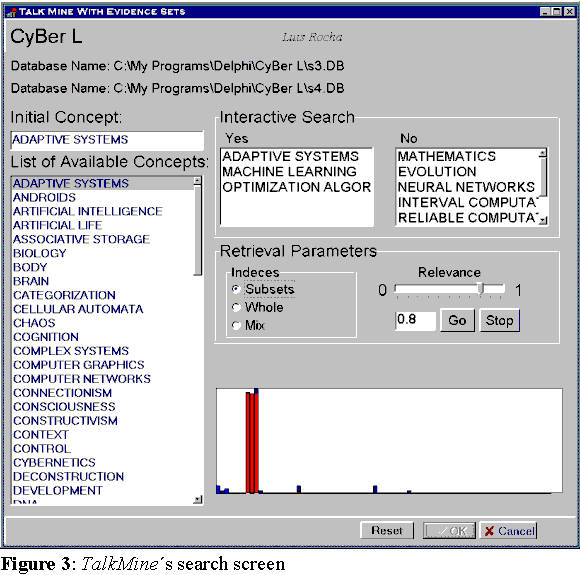
An application named TalkMine was developed that implements the above specified system. The example shown below refers to a database of 150 books. From the pool of 150 books three databases were created by randomly picking books from this pool with equal probability. Each sub-database is comprised of about 50 books, some of which exist in more than one of the sub-databases. Book records are the properties of the system described above. The fields created for these records were Title, Date, Authors, Publisher, plus 6 key-words describing the contents of the books. These keywords are the concepts of the system described above. Naturally, many of these keywords overlap. From the 150 books, 89 keywords were identified. Thus the system has 89 concepts and 150 properties. Figure 4 shows TalkMine's result screen. Two databases are selected S3.DBD and S4.DBD. In this case the initial concept to start the search was "ADAPTIVE SYSTEMS". The concepts (key-words) used in the question-answering process are shown in two different boxes for questions receiving "YES" and "NO" responses respectively.
TalkMine implements the contextual construction of short-term categories from several long-term relational structures as described above. It is based on prototypical categories represented by evidence sets defined in section 5. The long-term distributed memory structure implements the connectionist aspects of cognitive systems. It is this structure that ultimately dictates how categories are constructed. The categories constructed are short-term structures not stored in any location, but constructed "on the hoof" as the system relates its several sub-networks to the interaction (conversation) users provide. Its syntax is based on evidence sets and their extended theory of approximate reasoning. Semantics is established in accordance to the system's internal distributed semi-metrics, and how it pragmatically relates to the users needs. Furthermore, TalkMine explores contextual conflicting uncertainty as a source of artificial category construction, since the selection of concepts for the question-answering process is based on reducing the total uncertainty present in learned categories. More details about TalkMine can be found in Rocha [1997b].
The evidence set question-answering system of section 9 models the construction of the prototypical effects discussed in section 4. Such "on the hoof" construction of categories triggered by interaction with users, allows several distributed networks to be searched simultaneously, temporarily generating categories that are not really stored in any location. The short-term categories bridge together a number of possibly unrelated contexts, which in turn creates new associations in the individual databases that would never occur within their own limited context. Therefore, the construction of short-term linguistic categories in this artificial system, implements a sort of structural perturbation of long-term distributed associations. It is in fact a system of recontextualization of otherwise contextually constrained, independent distributed networks.
This transference of information across dissimilar contexts through short-term categorization models some aspects of what metaphor offers to human cognition: the ability to discern correspondence in non-similar concepts [Holyoak and Thagard, 1995; Henry, 1995]. Consider the following example. Two distinct databases are going to be searched using the system described above. One database contains the books of an institution devoted to the study of computational complex adaptive systems (e.g. the library of the Santa Fe Institute), and the other the books of a Philosophy of Biology department . I am interested in the concepts of Genetics and Natural Selection. If I were to conduct this search a number of times, due to my own interests, the learned category obtained would certainly contain other concepts such as Adaptive Computation, Genetic Algorithms, etc. Let me assume that the concept of Genetic Algorithms does not initially exist in the Philosophy of Biology library. After I conduct this search a number of times, the concept of Genetic Algorithms is created in this library, even though it does not contain any books in this area. However, with my continuing to perform this search over and over again, the concept of Genetic Algorithms becomes highly associated with Genetics and Natural Selection, in a sense establishing a metaphor for these concepts. From this point on, users of the Philosophy of Biology library, by entering the keyword Genetic Algorithms would have their own data retrieval system output books ranging from "The Origin of Species" to treatises on Neo-Darwinism - at which point they would probably bar me from using their networked database! Because of the Evidence Set system of short-term categorization that uses existing, fairly contextually independent distributed sub-networks, an ability to create correspondence between somewhat unrelated concepts is established.
Given a large number of sub-networks comprised of context-specific associations, the categorization system is able to create new categories that are not stored in any one location, changing the long-term memory banks in an open-ended fashion. Thus the linguistic categorization Evidence Set mechanism implements a system of open-ended structural perturbation of long-term networked memory. Open-endedness does not mean that the categorizing system is able to discern all possible details of its user environment, but that it can permutate all the associative information that it constructs in an open-ended manner. Each independent network has the ability to associate new knowledge in its own context (e.g. as more books are added to the libraries of the prior examples). To this, the categorization scheme adds the ability of open-ended associations built across networks and contexts. Therefore, a linguistic categorization mechanism as defined above, offers the ability to recontextualize lower level distributed memory banks, according to a pragmatic, consensual, interaction with an environment.
Barsalou, L. [1987]."The instability of graded structure: implications for the nature of concepts." In: Concepts and Conceptual Development: Ecological and Intellectual Factors in Categorization. U. Neisser (ed.). Cambridge University Press.
Campbell, D.T. [1974]."Evolutionary Epistemology." In: The Philosophy of Karl Popper. P.A. Schilpp (ed.). Open Court Publishers, pp. 413-463.
Clark, Andy [1993]. Associative Engines: Connectionism, Concepts, and Representational Change. MIT Press.
Dempster, A. [1967]."Upper and lower probabilities induced by multivalued mappings." Annals of Amthematical Statistics. vOL.. 38, PP. 325-339.
Dubois, D. and H. Prade [1985]."A note on measures of specificity for fuzzy sets." Int. J. of General Systems. Vol. 10, pp. 279-283.
Fodor, J. [1981]. Representations: Philosophical Essays on the Foundations of Cognitive Science. MIT Press.
Galvin, F. and S.D. Shore [1991]."Distance functions and topologies." The American Mathematical Monthly. Vol. 98, No. 7, pp. 620-623.
Gorzaczany, M.B. [1987]."A method of inference in approximate reasoning based on interval-valued fuzzy sets." Fuzzy Sets and Systems. Vol. 21, pp. 1-17.
Hampton, J. [1992]."Prototype models of concept representation." In: Categories and Concepts: Theoretical Views and Inductive Data Analysis. I. Van Mechelen, J.Hampton, R. Michalski, and P.Theuns. Academic Press.
Henry, C. and L.M. Rocha [1996]."Language theory: consensual selection of dynamics." In: Cybernetics and Systems: An International Journal. . Vol. 27, pp 541-553.
Henry, Charles [1995]."Universal Grammar." Communication and Cognition - Artificial Intelligence. Vol. 12, Nos. 1-2, pp. 45-62.
Holyoak, K.J. and P. Thagard [1995]. Mental Leaps: Analogy in Creative Thought. MIT Press.
Klir, G.J. and B. Yuan [1995]. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall.
Klir, George, J. [1991]. Facets of Systems Science. Plenum Press.
Klir, George, J. [1993]."Developments in uncertainty-based information." In: Advances in Computers. M. Yovits (Ed.). Vol. 36, pp. 255-332.
Lakoff, G. [1987]. Women, Fire, and Dangerous Things: What Categories Reveal about the Mind. University of Chicago Press.
Lorenz, K. [1971]."Knowledge, beliefs and freedom." In: Hierarchically Organized Systems in Theory and Practice. P. Weiss (ed.). Hafner.
Lorenz, K. [1981]. The Foundations of Ethology. Springer-Verlag.
Medin, D.L. and M.M. Schafer [1978]."A context theory of classification learning." In: Psychological Review. . Vol. 35, pp. 207-238.
Nakamura, K. and S. Iwai [1982]."A representation of analogical inference by fuzzy sets and its application to information retrieval systems." In: Fuzzy Information and Decision Processes. Gupta and Sanchez (Eds.). North-Holland, pp. 373-386.
Osherson, D. and E. Smith [1981]."On the adequacy of prototype theory as a theory of concepts." Cognition. Vol. 9, pp. 35-58.
Rocha, Luis, M. [1994]."Cognitive categorization revisited: extending interval valued fuzzy sets as simulation tools for concept combination." Proc. of the 1994 Int. Conference of NAFIPS/IFIS/NASA. IEEE Press, pp. 400-404.
Rocha, Luis M. [1995]."Interval based evidence sets." Proc. of ISUMA-NAFIPS'95. IEEE Press, pp. 624-629.
Rocha, Luis M. [1996]."Relative uncertainty: measuring uncertainty in discrete and nondiscrete domains." In: Proccedings of the NAFIPS'96. M. Smith et al (Eds.). IEEE Press. pp. 551-555.
Rocha, Luis M. [1997a]. Evidence Sets and Contextual Genetic Algorithms: Exploring Uncertainty, Context and Embodiment in Cognitive and biological Systems. PhD. Dissertation. State University of New York at Binghamton.
Rocha, Luis M. [1997b]."Relative uncertainty and evidence sets: a constructivist framework." International Journal of General Systems. Vol. 26, No. 1-2, pp. 35-61.
Rocha, Luis M. [1997c]. "Evidence Sets: Contextual Categories". In: Proceedings of the meeting on Control Mechanisms for Complex Systems, Physical Science Laboratory, New Mexico State University, Las Cruces, New Mexico, January 1997. M. Coombs (ed.). NMSU Press, pp. 339-357.
Rocha, Luis M., V. Kreinovich, and K. B. Kearfott [1996]."Computing uncertainty in interval based sets." In: Applications of Interval Computations. V. Kreinovich and K.B. Kearfott (Eds.). Kluwer Academic Publishers, pp. 337-380.
Rosch, E. [1975]."Cognitive representations of semantic categories." J. of Experimental Psychology. Vol. 104, pp. 27-48.
Rosch, E. [1978]."Principles of categorization." In: Cognition and Categorization. E. Rosch and B. Lloyd (Eds.). Hillsdale, pp. 27-48.
Shafer, G. [1976]. A Mathematical Theory of Evidence. Princeton University Press.
Smith, E. and D. Osherson [1984]."Conceptual combination with prototype concepts." Cognitive Science. Vol. 8, pp. 337-361.
Smith, E.E. and D.L. Medin [1981]. Categories and Concepts. Harvard University Press.
Turksen, B. [1986]."Interval valued fuzzy sets based on normal forms." Fuzzy Sets and Systems. Vol. 20, pp. 191-210.
Van Gelder, Tim [1991]. "What is the 'D' in 'PDP': a survey of the concept of distribution". In: Philosophy and Connectionist Theory. Eds. W. Ramsey et al. Lawrence Erlbaun.
Yager, R.R. [1979]."On the measure of fuzziness and negation. Part I: membership in the unit interval." Int. J. of General Systems. Vol. 5, pp. 221-229.
Yager, R.R. [1980]."On the measure of fuzziness and negation: Part II: lattices." Information and Control. Vol. 44, pp. 236-260.
Yen, John [1990]."Generalising the Dempster-Shafer theory to fuzzy sets." IEEE Transactions on Systems, Man, and Cybernetics. Vol. 20, pp. 559-570. Reprinted in Wang and Klir [1992], pp. 257-283.
1. The membership value of an element of an evidence set is independent of the membership values of others elements contained in the set.
2. This measure of distance calculated in a large network of nodes, is usually not a Euclidean metric because it does not observe the triangular inequality. In other words, the shortest distance between two nodes of the network might not be the direct path. This means that two nodes may be closer to each other when another node is associated with them. Such measures of distance are referred to as semi-metrics [Galvin and Shore, 1991].