Both MT and TT800 are variants of generalized FSRs (see Section 3.3)
based on the following linear recurrence
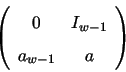
MT actually operates on 19937-bit words, and when it is implemented on 32-bit hardware, it requires a work area of 624 32-bit integers to store the whole word. Every time a random variate is requested, a consecutive 32-bit portion is extracted sequentially from the 19937-bit word and undergoes three XOR operations before output. The algorithm will generate another 19937-bit word when all of its 32-bit portions have been requested. Initial seed of MT is a 19937-bit word, which can be given by the first 624 outputs of ordinary 32-bit integer LCGs.
Most congruential-based generators uses prime numbers as the modulus to
achieve long periods. The authors of MT chose a special class of primes
called Mersenne prime, which is of form ![]() and
and ![]() in MT's case
, to create an RNG that can produce a theoretically 623-distributed sequence
(see Section 2.1). Longer periods are possible by using larger
Mersenne primes.
in MT's case
, to create an RNG that can produce a theoretically 623-distributed sequence
(see Section 2.1). Longer periods are possible by using larger
Mersenne primes.