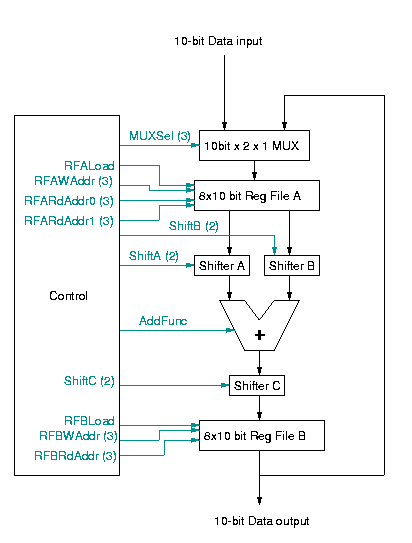
Figure 1: Block diagram of IDCT system
This report discusses the specifications and design of a Discrete Cosine Transform decoder. Since the DCT is used in many video, image, and audio compression standards (such as MPEG and JPEG), a DCT decoder is the heart of many decompression systems. First, this report will discuss the overall specification and function of the circuit. The second part contains details about the chip's operation and design. Finally, each block of the circuit will be discussed in detail.
This chip will perform an approximation of the one dimensional Inverse Discrete Cosine Transformation on eight 10-bit signed integers. The operation of the chip is summarized as follows:
These approximations dramatically reduce the complexity of our circuit by eliminating the need for a multiplier. Instead of multipliers, two simple 1-bit bidirectional shifters are used in the new design to multiply using these approximations. (c1 and c2 require right shifting once, then right shifting again and adding to results of the two shifts, but our design already supports this.) Of course these approximations cause a less accurate result, and their effect is discussed in the Appendix to this report.
The output pins of the chip will be:

In the block diagram, the black lines represent 10-bit signals, while gray lines represent one or more control signals. The block diagram presents an overview of the system, and specific details of each block are discussed in section IV. The block diagram contains the following parts:
In this section, each of the blocks in the above block diagram are discussed in detail.
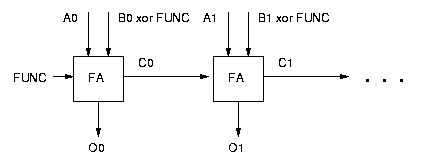
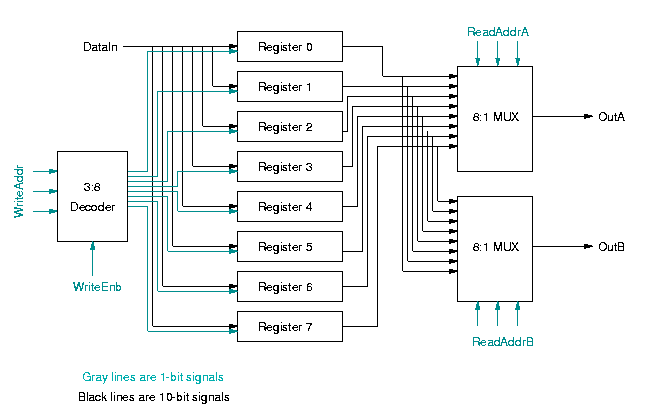
Each register has a load input, indicating whether it is to latch the input data on the next clock cycle, and an output with its current contents. A multiplexer is used to route the correct register outputs to ROut0 and ROut1. A decoder is used to specify the LOAD input to each register based on the values of WADDR and Load.
Each 10-bit register will require 10 D flip-flops, and a few simple gates to load them based on the LOAD input.
I converted the IDCT algorithm[3] into a state table (which is in the Appendix of this report). Each row of this table represents a state, and each column represents the output of the machine during this state. The states are always visited in order from first to last. This table has 26 output bits and 80 states.
I was somewhat alarmed at the large number of states required, but more efficient state tables are possible. By taking advantage of operations that can be performed concurrently, I was able to reduce the state table to 48 states. However, the control circuit will still be a challenge to implement. The counter will consist of an adder and a register, which will have already been implemented for other blocks. The combinational portion of the FSM will be more complex, since there are 48 states and 26 output bits. However, there are many don't-cares (represented by x's) in the state tables, so many of the output bit equations should be simple.
To test this, I modified the Berkeley MPEG_PLAY source code to use the approximations proposed for
this system. This provides a subjective evaluation of the effects of the approximations. The modified
source code is available
in this directory (the file floatdct.c has most of the modifications). The results of the
test are shown in Figure 4. Figure 4a is the output of the original MPEG_PLAY, while Figure 4b
uses the approximations. Note that while the degradation is very noticable, the image
is still of an acceptable quality.
V. Appendix
Effect of coefficient approximations on IDCT
It is obvious that the coefficient approximations in the IDCT algorithm will effect the accuracy
of the results. Since the error in some of these approximations is close to 50%, if the values
of the DCT are large, the error will be very noticable in the results. However, when DCT is used
for compressing images, most of the higher DCT coefficients are close to zero. Therefore the
effect of these approximations in an actual application is probably significant, but the approximation
is good enough that the image is still visable.

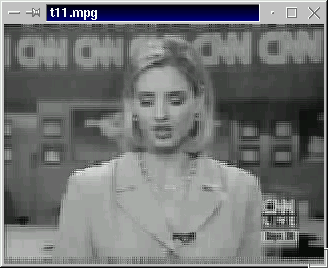
Figure 4a (left): Frame decompressed with normal IDCT; 4b (right): with approximated IDCTControl State Table (Naive version)
M R R R R R R R S S S A R
U F F F F F F F A B C D E
X A A A A B B B D A
S L W R R L W R M D
E D A A A D A A D Y
L 0 1
#### load data from input (8 cycles)
0 1 001 xxx xxx x xxx xxx xx xx xx x 0
0 1 010 xxx xxx x xxx xxx xx xx xx x 0
0 1 100 xxx xxx x xxx xxx xx xx xx x 0
0 1 110 xxx xxx x xxx xxx xx xx xx x 0
0 1 000 xxx xxx x xxx xxx xx xx xx x 0
0 1 111 xxx xxx x xxx xxx xx xx xx x 0
0 1 101 xxx xxx x xxx xxx xx xx xx x 0
0 1 011 xxx xxx x xxx xxx xx xx xx x 0
#### compute S2 array
### compute s2[0]
## compute c1*s1[0]
x 0 xxx 000 xxx 1 000 xxx 11 01 00 0 0 # RFb0 <- RFa0 / 2
1 1 000 xxx xxx 0 xxx 000 xx xx xx x 0 # RFa0 <- RFb0
x 0 xxx 000 000 1 000 xxx 11 00 00 0 0 # RFb0 <- RFa0 / 2 + RFa0
1 1 000 xxx xxx 0 xxx 000 xx xx xx x 0 # RFa0 <- RFb0
## compute c2*s1[1]
x 0 xxx 001 xxx 1 001 xxx 11 01 00 0 0 # RFb1 <- RFa1 / 2
1 1 001 xxx xxx 0 xxx 001 xx xx xx x 0 # RFa1 <- RFb1
x 0 xxx 001 001 1 001 xxx 11 00 00 0 0 # RFb1 <- RFa1 / 2 + RFa1
1 1 001 xxx xxx 0 xxx 001 xx xx xx x 0 # RFa1 <- RFb1
## s2[0]=(c1*s1[0] + c2*s1[1]) * 2
x 0 xxx 000 001 1 000 xxx 00 00 10 0 0 # RFb0 <- (RFa0 + RFa1) * 2
## s2[2]=(c1*s1[1] - c2*s1[0]) * 2
x 0 xxx 000 001 1 000 xxx 00 00 10 1 0 # RFb2 <- (RFa0 - RFa1) * 2
## s2[1]=(c5*s1[4] + c6*s1[5]) * 2
x 0 xxx 100 101 1 001 xxx 00 11 10 0 0 # RFb1 <- (RFa4 + RFa5/2) * 2
## s2[3]=(c5*s1[5] - c6*s1[4]) * 2
x 0 xxx 101 100 1 011 xxx 00 11 10 1 0 # RFb3 <- (RFa5 - RFa4/2) * 2
## s2[4]=(c3*s1[2] + c4*s1[3]) * 2
x 0 xxx 010 011 1 100 xxx 00 11 10 0 0 # RFb4 <- (RFa2 + RFa3/2) * 2
## s2[5]=(c7*s1[6] + c8*s1[7]) * 2
x 0 xxx 110 111 1 101 xxx 11 11 10 0 0 # RFb5 <- (RFa6/2 + RFa7/2) * 2
## s2[6]=(c3*s1[3] - c4*s1[2]) * 2
x 0 xxx 011 010 1 110 xxx 00 11 10 1 0 # RFb6 <- (RFa3 - RFa2/2) * 2
## s2[7]=(c7*s1[7] - c8*s1[6]) * 2
x 0 xxx 111 110 1 111 xxx 11 11 10 1 0 # RFb7 <- (RFa7/2 - RFa6/2) * 2
1 1 000 xxx xxx 0 xxx 000 xx xx xx x 0 # RFa0 <- RFb0
1 1 001 xxx xxx 0 xxx 001 xx xx xx x 0 # RFa1 <- RFb1
1 1 010 xxx xxx 0 xxx 010 xx xx xx x 0 # RFa2 <- RFb2
1 1 011 xxx xxx 0 xxx 011 xx xx xx x 0 # RFa3 <- RFb3
1 1 100 xxx xxx 0 xxx 100 xx xx xx x 0 # RFa4 <- RFb4
1 1 101 xxx xxx 0 xxx 101 xx xx xx x 0 # RFa5 <- RFb5
1 1 110 xxx xxx 0 xxx 110 xx xx xx x 0 # RFa6 <- RFb6
1 1 111 xxx xxx 0 xxx 111 xx xx xx x 0 # RFa7 <- RFb7
#### compute S3 array
## s3[0]=(s2[4] + s2[5]) / 2
x 0 xxx 100 101 1 000 xxx 00 00 11 0 0 # RFb0 <- (RFa4 + RFa5) / 2
## s3[1]=(s2[6] - s2[7]) / 2
x 0 xxx 110 111 1 001 xxx 00 00 11 1 0 # RFb1 <- (RFa6 - RFa7) / 2
## s3[3]=(s2[4] - s2[5]) / 2
x 0 xxx 100 101 1 011 xxx 00 00 11 1 0 # RFb3 <- (RFa4 - RFa5) / 2
## s3[7]=(s2[6] + s2[7]) / 2
x 0 xxx 110 111 1 111 xxx 00 00 11 1 0 # RFb1 <- (RFa6 + RFa7) / 2
x 0 xxx 000 xxx 1 010 xxx 00 00 00 0 0 # RFb2 <- RFa0
x 0 xxx 001 xxx 1 100 xxx 00 00 00 0 0 # RFb4 <- RFa1
x 0 xxx 010 xxx 1 101 xxx 00 00 00 0 0 # RFb5 <- RFa2
x 0 xxx 011 xxx 1 110 xxx 00 00 00 0 0 # RFb6 <- RFa3
1 1 000 xxx xxx 0 xxx 000 xx xx xx x 0 # RFa0 <- RFb0
1 1 001 xxx xxx 0 xxx 001 xx xx xx x 0 # RFa1 <- RFb1
1 1 010 xxx xxx 0 xxx 010 xx xx xx x 0 # RFa2 <- RFb2
1 1 011 xxx xxx 0 xxx 011 xx xx xx x 0 # RFa3 <- RFb3
1 1 100 xxx xxx 0 xxx 100 xx xx xx x 0 # RFa4 <- RFb4
1 1 101 xxx xxx 0 xxx 101 xx xx xx x 0 # RFa5 <- RFb5
1 1 110 xxx xxx 0 xxx 110 xx xx xx x 0 # RFa6 <- RFb6
1 1 111 xxx xxx 0 xxx 111 xx xx xx x 0 # RFa7 <- RFb7
#### compute S4 array
#### (no computation necessary since our approximation
#### of c9 is 1)
#### compute S5 array
## s5[0]=(s4[2] + s4[4]) / 2
x 0 xxx 010 100 1 000 xxx 00 00 11 0 0 # RFb0 <- (RFa2 + RFa4) / 2
## s5[2]=(s4[5] + s4[3]) / 2
x 0 xxx 101 011 1 010 xxx 00 00 11 0 0 # RFb2 <- (RFa5 + RFa3) / 2
## s5[3]=(s4[6] + s4[7]) / 2
x 0 xxx 110 111 1 011 xxx 00 00 11 0 0 # RFb3 <- (RFa6 + RFa7) / 2
## s5[4]=(s4[2] - s4[4]) / 2
x 0 xxx 010 100 1 100 xxx 00 00 11 1 0 # RFb4 <- (RFa2 + RFa4) / 2
## s5[6]=(s4[5] - s4[3]) / 2
x 0 xxx 101 011 1 110 xxx 00 00 11 1 0 # RFb6 <- (RFa5 + RFa3) / 2
## s5[7]=(s4[6] - s4[7]) / 2
x 0 xxx 110 111 1 111 xxx 00 00 11 1 0 # RFb7 <- (RFa6 + RFa7) / 2
x 0 xxx 000 xxx 1 001 xxx 00 00 00 0 0 # RFb1 <- RFa0
x 0 xxx 001 xxx 1 101 xxx 00 00 00 0 0 # RFb5 <- RFa1
1 1 000 xxx xxx 0 xxx 000 xx xx xx x 0 # RFa0 <- RFb0
1 1 001 xxx xxx 0 xxx 001 xx xx xx x 0 # RFa1 <- RFb1
1 1 010 xxx xxx 0 xxx 010 xx xx xx x 0 # RFa2 <- RFb2
1 1 011 xxx xxx 0 xxx 011 xx xx xx x 0 # RFa3 <- RFb3
1 1 100 xxx xxx 0 xxx 100 xx xx xx x 0 # RFa4 <- RFb4
1 1 101 xxx xxx 0 xxx 101 xx xx xx x 0 # RFa5 <- RFb5
1 1 110 xxx xxx 0 xxx 110 xx xx xx x 0 # RFa6 <- RFb6
1 1 111 xxx xxx 0 xxx 111 xx xx xx x 0 # RFa7 <- RFb7
#### compute d array
## d[0]=(s5[0] + s5[1]) / 2
x 0 xxx 010 100 1 000 xxx 00 00 11 0 0 # RFb0 <- (RFa0 + RFa1) / 2
## d[1]=(s5[2] - s5[3]) / 2
x 0 xxx 010 100 1 000 xxx 00 00 11 1 0 # RFb1 <- (RFa2 - RFa3) / 2
## d[2]=(s5[2] + s5[3]) / 2
x 0 xxx 101 011 1 010 xxx 00 00 11 0 0 # RFb2 <- (RFa2 + RFa3) / 2
## d[3]=(s5[4] - s5[5]) / 2
x 0 xxx 110 111 1 011 xxx 00 00 11 1 0 # RFb3 <- (RFa4 - RFa5) / 2
## d[4]=(s5[4] + s5[5]) / 2
x 0 xxx 010 100 1 100 xxx 00 00 11 0 0 # RFb4 <- (RFa4 + RFa5) / 2
## d[5]=(s5[6] + s5[7]) / 2
x 0 xxx 010 100 1 000 xxx 00 00 11 0 0 # RFb5 <- (RFa6 + RFa7) / 2
## d[6]=(s5[6] - s5[7]) / 2
x 0 xxx 101 011 1 110 xxx 00 00 11 1 0 # RFb6 <- (RFa6 - RFa7) / 2
## d[7]=(s5[0] - s5[1]) / 2
x 0 xxx 110 111 1 111 xxx 00 00 11 1 0 # RFb7 <- (RFa0 - RFa1) / 2
#### output
x 0 xxx xxx xxx 0 xxx 000 xx xx xx x 1
x 0 xxx xxx xxx 0 xxx 001 xx xx xx x 0
x 0 xxx xxx xxx 0 xxx 010 xx xx xx x 0
x 0 xxx xxx xxx 0 xxx 011 xx xx xx x 0
x 0 xxx xxx xxx 0 xxx 100 xx xx xx x 0
x 0 xxx xxx xxx 0 xxx 101 xx xx xx x 0
x 0 xxx xxx xxx 0 xxx 110 xx xx xx x 0
x 0 xxx xxx xxx 0 xxx 111 xx xx xx x 0
M R R R R R R R S S S A
U F F F F F F F A B C D
X A A A A B B B D
S L W R R L W R M
E D A A A D A A D
L 0 1
Control State Table (More efficient version)
#M R R R R R R R S S S A R
#U F F F F F F F A B C D E
#X A A A A B B B D A
#S L W R R L W R M D
#E D A A A D A A D Y
#L 0 1
#### load data from input (8 cycles)
0 1 100 xxx xxx x xxx xxx xx xx xx x 0
0 1 000 000 xxx 1 000 xxx 11 01 00 0 0 # RFb0 <- RFa0 / 2
0 1 101 001 xxx 1 001 xxx 11 01 00 0 0 # RFb1 <- RFa1 / 2
0 1 111 xxx xxx x xxx xxx xx xx xx x 0
0 1 010 xxx xxx x xxx xxx xx xx xx x 0
0 1 110 xxx xxx x xxx xxx xx xx xx x 0
0 1 011 xxx xxx x xxx xxx xx xx xx x 0
0 1 101 xxx xxx x xxx xxx xx xx xx x 0
#### compute S2 array
### compute s2[0]
## compute c1*s1[0]
1 1 000 xxx xxx 0 xxx 000 xx xx xx x 0 # RFa0 <- RFb0
1 1 001 000 000 1 000 001 11 00 00 0 0 # RFb0 <- RFa0 / 2 + RFa0;RFa1 <- RFb1
1 1 000 001 001 1 001 000 11 00 00 0 0 # RFa0 <- RFb0; RFb1 <- RFa1 / 2 + RFa1
## compute c2*s1[1]
1 1 001 xxx xxx 0 xxx 001 xx xx xx x 0 # RFa1 <- RFb1
## s2[0]=(c1*s1[0] + c2*s1[1]) * 2
x 0 xxx 000 001 1 000 xxx 00 00 10 0 0 # RFb0 <- (RFa0 + RFa1) * 2
## s2[2]=(c1*s1[1] - c2*s1[0]) * 2
x 0 xxx 000 001 1 000 xxx 00 00 10 1 0 # RFb2 <- (RFa0 - RFa1) * 2
## s2[1]=(c5*s1[4] + c6*s1[5]) * 2
1 1 000 100 101 1 001 000 00 11 10 0 0 # RFb1 <- (RFa4 + RFa5/2) * 2; RFa0 <- RFb0
## s2[3]=(c5*s1[5] - c6*s1[4]) * 2
1 1 001 101 100 1 011 001 00 11 10 1 0 # RFb3 <- (RFa5 - RFa4/2) * 2; RFa1 <- RFb1
## s2[4]=(c3*s1[2] + c4*s1[3]) * 2
x 0 xxx 010 011 1 100 xxx 00 11 10 0 0 # RFb4 <- (RFa2 + RFa3/2) * 2
## s2[5]=(c7*s1[6] + c8*s1[7]) * 2
x 0 101 110 111 1 101 101 11 11 10 0 0 # RFb5 <- (RFa6/2 + RFa7/2) * 2; RFa5 <- RFb5
## s2[6]=(c3*s1[3] - c4*s1[2]) * 2
x 0 100 011 010 1 110 100 00 11 10 1 0 # RFb6 <- (RFa3 - RFa2/2) * 2; RFa4 <- RFb4
## s2[7]=(c7*s1[7] - c8*s1[6]) * 2
1 1 110 111 110 1 111 110 11 11 10 1 0 # RFb7 <- (RFa7/2 - RFa6/2) * 2; RFa6 <- RFb6
#### compute S3 array
## s3[0]=(s2[4] + s2[5]) / 2
1 1 111 100 101 1 000 111 00 00 11 0 0 # RFb0 <- (RFa4 + RFa5) / 2; RFa7 <- RFb7
## s3[1]=(s2[6] - s2[7]) / 2
1 1 011 110 111 1 001 011 00 00 11 1 0 # RFb1 <- (RFa6 - RFa7) / 2; RFa3 <- RFb3
## s3[3]=(s2[4] - s2[5]) / 2
1 1 010 100 101 1 011 010 00 00 11 1 0 # RFb3 <- (RFa4 - RFa5) / 2; RFa2 <- RFb2
## s3[7]=(s2[6] + s2[7]) / 2
x 0 xxx 110 111 1 111 xxx 00 00 11 1 0 # RFb1 <- (RFa6 + RFa7) / 2
1 1 111 000 xxx 1 010 111 00 00 00 0 0 # RFb2 <- RFa0; RFa7 <- RFb7
1 1 000 001 xxx 1 100 000 00 00 00 0 0 # RFb4 <- RFa1; RFa0 <- RFb0
1 1 100 010 xxx 1 101 100 00 00 00 0 0 # RFb5 <- RFa2; RFa4 <- RFb4
1 1 101 011 xxx 1 110 101 00 00 00 0 0 # RFb6 <- RFa3; RFa5 <- RFb5
1 1 010 xxx xxx 0 xxx 010 xx xx xx x 0 # RFa2 <- RFb2
#### compute S4 array
#### (no computation necessary since our approximation
#### of c9 is 1)
#### compute S5 array
## s5[0]=(s4[2] + s4[4]) / 2
1 1 011 010 100 1 000 011 00 00 11 0 0 # RFb0 <- (RFa2 + RFa4) / 2; RFa3 <- RFb3
## s5[2]=(s4[5] + s4[3]) / 2
1 1 110 101 011 1 010 110 00 00 11 0 0 # RFb2 <- (RFa5 + RFa3) / 2; RFa6 <- RFb6
## s5[3]=(s4[6] + s4[7]) / 2
1 1 001 110 111 1 011 001 00 00 11 0 0 # RFb3 <- (RFa6 + RFa7) / 2; RFa1 <- RFb1
## s5[4]=(s4[2] - s4[4]) / 2
x 0 xxx 010 100 1 100 xxx 00 00 11 1 0 # RFb4 <- (RFa2 + RFa4) / 2
## s5[6]=(s4[5] - s4[3]) / 2
1 1 100 101 011 1 110 100 00 00 11 1 0 # RFb6 <- (RFa5 + RFa3) / 2; RFa4 <- RFb4
## s5[7]=(s4[6] - s4[7]) / 2
1 1 011 110 111 1 111 011 00 00 11 1 0 # RFb7 <- (RFa6 + RFa7) / 2; RFa3 <- RFb3
1 1 110 000 xxx 1 001 110 00 00 00 0 0 # RFb1 <- RFa0; RFa6 <- RFb6
1 1 111 001 xxx 1 101 111 00 00 00 0 0 # RFb5 <- RFa1; RFa7 <- RFb7
1 1 000 xxx xxx 0 xxx 000 xx xx xx x 0 # RFa0 <- RFb0
1 1 001 xxx xxx 0 xxx 001 xx xx xx x 0 # RFa1 <- RFb1
1 1 101 xxx xxx 0 xxx 101 xx xx xx x 0 # RFa5 <- RFb5
#### compute d array and output
## d[0]=(s5[0] + s5[1]) / 2
1 1 010 010 100 1 000 010 00 00 11 0 0 # RFb0 <- (RFa0 + RFa1) / 2; RFa2 <- RFb2
## d[1]=(s5[2] - s5[3]) / 2
x 0 xxx 010 100 1 000 000 00 00 11 1 1 # RFb1 <- (RFa2 - RFa3) / 2
## d[2]=(s5[2] + s5[3]) / 2
x 0 xxx 101 011 1 010 001 00 00 11 0 0 # RFb2 <- (RFa2 + RFa3) / 2
## d[3]=(s5[4] - s5[5]) / 2
x 0 xxx 110 111 1 011 010 00 00 11 1 0 # RFb3 <- (RFa4 - RFa5) / 2
## d[4]=(s5[4] + s5[5]) / 2
x 0 xxx 010 100 1 100 011 00 00 11 0 0 # RFb4 <- (RFa4 + RFa5) / 2
## d[5]=(s5[6] + s5[7]) / 2
x 0 xxx 010 100 1 000 100 00 00 11 0 0 # RFb5 <- (RFa6 + RFa7) / 2
## d[6]=(s5[6] - s5[7]) / 2
x 0 xxx 101 011 1 110 101 00 00 11 1 0 # RFb6 <- (RFa6 - RFa7) / 2
## d[7]=(s5[0] - s5[1]) / 2
x 0 xxx 110 111 1 111 110 00 00 11 1 0 # RFb7 <- (RFa0 - RFa1) / 2
#output
x 0 xxx xxx xxx 0 xxx 111 xx xx xx x 0
#M R R R R R R R S S S A
#U F F F F F F F A B C D
#X A A A A B B B D
#S L W R R L W R M
#E D A A A D A A D
#L 0 1
VI. References
[1] Loeffler, Ligtenberg and Moschytz, "Practical Fast 1-D DCT
Algorithms with 11 Multiplications", Proceedings of the International
Conference on Acoustics, Speech, and Signal Processing 1989, pp. 988-991.
[2] Gonzalez, Rafael C. and Richard E. Woods. Digital Image
Processing. New York: Addison-Wesley Publishing Company, 1993.
[3] Web Page: http://www.cs.uow.edu.au/people/nabg/MPEG/IDCT.html