Allen-Cocke Interval Partitioning of Flow Graphs

The term interval used in the sense of Allen-Cocke partitioning of a graph is different from the term interval graph that is often used to refer to a specific type of graph. An interval graph consists of nodes that denote ranges of real numbers and edges that connect nodes corresponding to intersecting ranges. Such interval graphs are widely used in modeling resource scheduling problems. The interference graph used in register allocation using graph coloring could be thought of as an interval graph. In contrast, the Allen-Cocke intervals are sets of nodes that satisfy certain properties.

An Interval in a flow graph, G, is defined as a set I of blocks such that:

  1. There is a node h ∈ I, called the head of I, which lies on every control path from a block outside I to a block within I, i.e., h dominates all nodes in I — {h}.
  2. I is connected.
  3. I — {h} is cycle-free, i.e., all cycles within I must contain h.

For a control flow node x, define PRED(x) to be the set of all predecessors of x and SUCC(x) as the set of all the successors of x. PRED and SUCC can also be defined for a set X of nodes using the obvious extension:

PRED(X) = {PRED(x) | x ∈ X}
SUCC(X) = {SUCC(x) | x ∈ X}

The algorithm to construct the maximal interval with head h relies on adding new nodes to the set as long as all the predecessors of the new node lie entirely within the set. 

Algorithm Max_Int
Input: Head node h
Output: Maximal interval with the head node h

I ← h
while ∃ x ∈ (SUCC(I) — I) such that PRED(x) ⊆ I
  {
     I ← I ∪ {x}
  }
return I

Theorem 1: The Max_Int algorithm correctly computes the maximal interval for a given head h.
Proof: The proof relies on two lemmas:
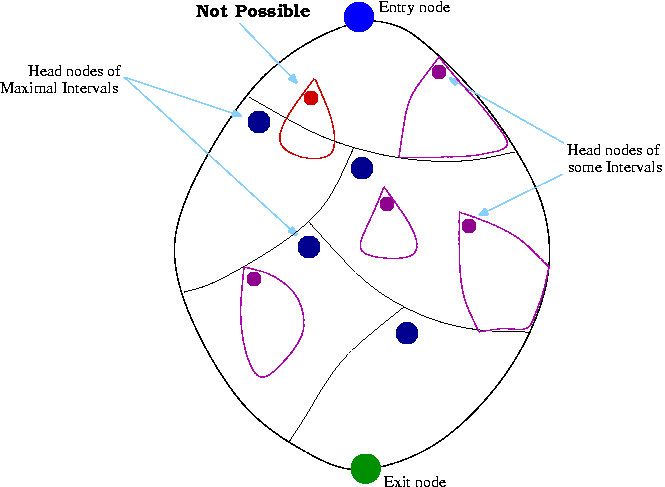
  1. Lemma 1: There is a unique maximal interval for a given head h.
  2. Lemma 2: The nodes added by the Max_Int algorithm are exactly the nodes that constitute the maximal interval for the given head.
Proof of Lemma 1

Suppose that there is not a unique maximal interval so that there are at least two distinct maximal intervals I1 and I2 with the head h. Clearly, neither I1 nor I2 is a subset of the other. Why? Therefore, there must be at least one node in I1 that is not in I2. Call this node n. Define PATH+(n) to be the set of all nodes on all the paths from h to n. Formally,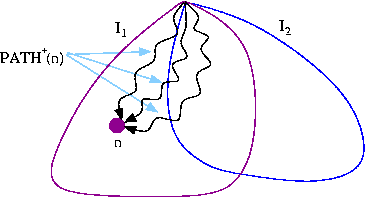
PATH+(n) = {x | x ∈ some path from h to n}
We claim that it is possible to extend the interval I2 by adding PATH+(n) to it. In other words, the set,
I  =  I2 ∪ PATH+(n)
is an interval.

  1. There is no path to a node in I from outside I that does not go through h. This is true for all nodes in I2. Any other node included in I came from I1, so there could not be a path to it from outside I1 that does not go through h. Moreover, there cannot be any path to any node in PATH+(n) from I1— PATH+(n) that does not go through h. If there was such a path from a node q in I1 — PATH+(n) to a node r in PATH+(n), then h→+q→+r→*n would be a path from h to n and, by definition, q would be in PATH+(n), a contradiction.
  2. The set I is connected because all nodes in I are reachable from h.
  3. The set I — {h} is cycle-free. All nodes belonging to I2 certainly satisfy this property. Since all other nodes in I belong to I1 they must also satisfy this property.

Since all three interval conditions are satisfied, the set I is an interval. Therefore, either I2 is not a maximal interval or there is no node n that belongs to I1 but not to I2. In the latter case I1 must be identical to I2, and hence there is a unique maximal interval.
Proof of Lemma 2
Given Lemma 1 it makes sense to talk about the maximal interval for a given head h. In order to show that the Max_Int algorithm builds the maximal interval we need to prove that the criteria it uses to add new nodes to expand its set allow the algorithm to pick exactly the nodes in the maximal interval, i.e., it picks all, and only, the nodes in the maximal interval. We will say that the nodes that meet the criteria used by the algorithm to augment its set satisfy the pick condition. Also, we will say that a node that can be added to an existing interval while the maintaining the interval property of the expanded set satisfies the interval condition. We prove the lemma by proving that:
pick condition ⇔ interval condition
It is clear that if that is the case then the algorithm will pick exactly the nodes that go into the maximal interval for the head h. We prove the above statement by proving each direction of the arrow.
pick condition ⇒ interval condition
A node satisfies the pick conditions if it is a successor of any node in the already built set and has all its predecessors within the already built set. Let's call the already built set S, and the node that is selected according to the pick conditions, n. We want to show that given that S is an interval, S ∪ n is an interval (which is exactly the definition of n satisfying the interval condition). This will prove by induction that the algorithm builds a valid interval at every iteration. How? All predecessors of n lie within S. All paths from any node outside S to any node within S go through h, hence all paths to n must also go through h. Since n is a successor of some node in S it is connected to S, implying that S ∪ n is connected. Finally, S ∪ n — {h} cannot contain any cycle, because if it does then there must be a path from n to a node in S — h without involving h, violating the assumption that S is an interval. Thus, the set S — h satisfies all three conditions of an interval and, therefore, is an interval.
interval condition ⇒ pick condition
For this direction we want to prove that if a node n satisfies all the conditions to be added to an existing interval then it will be picked by the algorithm. Suppose that S is the interval set that has already been built. Then S ∪ {n} is a valid interval. This means that S ∪ {n} is connected, and therefore at least one predecessor of n must be in S. Moreover, no predecessor of n can be outside S. If there was such a predecessor then there would be a path from a node outside the interval S ∪ {n} to a node inside it (i.e., n) without going through the head h, leading to a contradiction. Thus n satisfies both the pick conditions.

Given the two lemmas, it immediately follows that the algorithm Max_Int builds the unique maximal intervals for a given head node h.

The partitioning algorithm calls Max_Int to repeatedly build maximal intervals. This results in minimal interval partitioning of the given flow graph, i.e., partitioning into minimal number of maximal sized intervals. The following theorem proves this claim.

Theorem 2: The Allen-Cocke interval partitioning algorithm generates minimal number of partitions of a flow graph with the maximal sized intervals.

Proof: The proof of the theorem relies on the observation that no interval can ever span multiple maximal intervals generated by the Max_Int algorithm. In other words, an interval shown in red in the figure is not possible. This can easily be shown by contradiction. The proof is left as an exercise. Thus, any other partitioning of the graph will result in a larger number of intervals.

B629, Arun Chauhan, Department of Computer Science, Indiana University