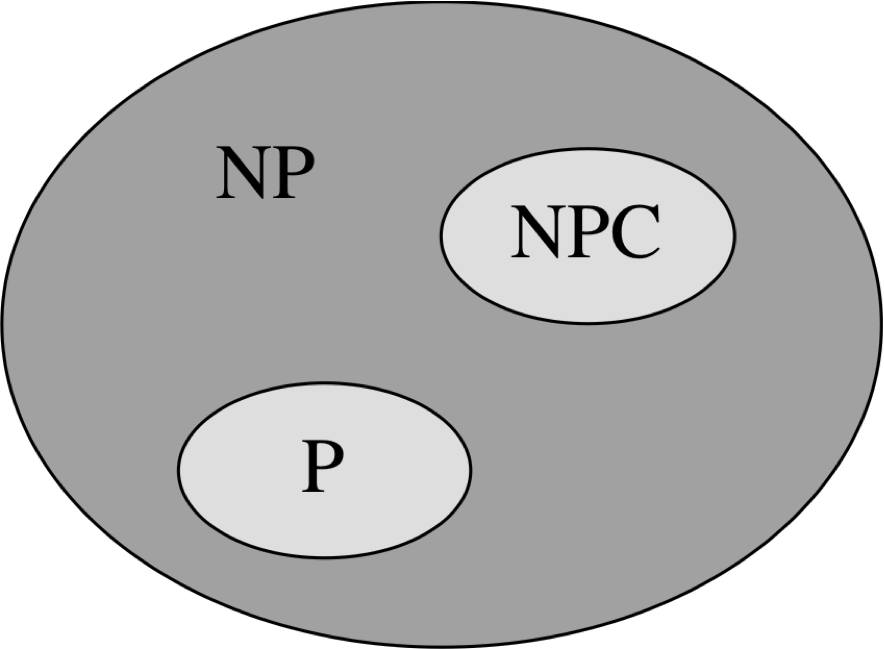
NP-Complete Problems
B403: Introduction to Algorithm Design and Analysis
Key Ideas
- Polynomial-time algorithms are interesting
- Most polynomial-time algorithms tend to have running times in low-degree polynomials
- Polynomials are closed under composition
- New discoveries often reduce the algorithmic complexities by lowering the degree of the polynomial representing the running time
- We talk about only decision problems
- Even though we are often interested in solving optimization problems, if the decision problem is hard then so is the optimization problem
- NP denotes Nondeterministic Polynomial time; there are three equivalent views of nondeterminism
- Polynomial running time with unbounded parallelism
- Polynomial running time with an “oracle” that always “guesses” the right solution
- Polynomial running time to verify whether a certificate represents a valid solution
CAVEAT: Specific Instances May Be Easy to Solve
- Problem: “Does a graph G have Hamiltonian Cycle?”
NP-complete in general, but any bipartite graph with odd number of vertices is nonhamiltonian - Problem: “Is a given Boolean formula satisfiable?”
NP-complete in general, but easy to solve for formulas in 2-CNF form
Small Changes can Make Problems Much Harder
- Shortest vs longest simple paths
- Euler tour vs Hamiltonian cycle
- 2-CNF satisfiability vs 3-CNF satisfiability
Key Definitions
A problem is in NP if there exists a polynomial-time algorithm to verify a certificate for the problem.
A problem is NP-complete if it is NP, and every other problem in NP can be reduced to it in polynomial time.
Polynomial-time Reductions to Prove Completeness
If every instance of known NP-complete problem, A, can be reduced to an instance of another problem, B, such that:
- The reduction takes a polynomial amount of time; and
- The answer to A can be obtained directly from the answer to B;
then B is NP-complete. Remember, A and B are decision problems.

Roadmap
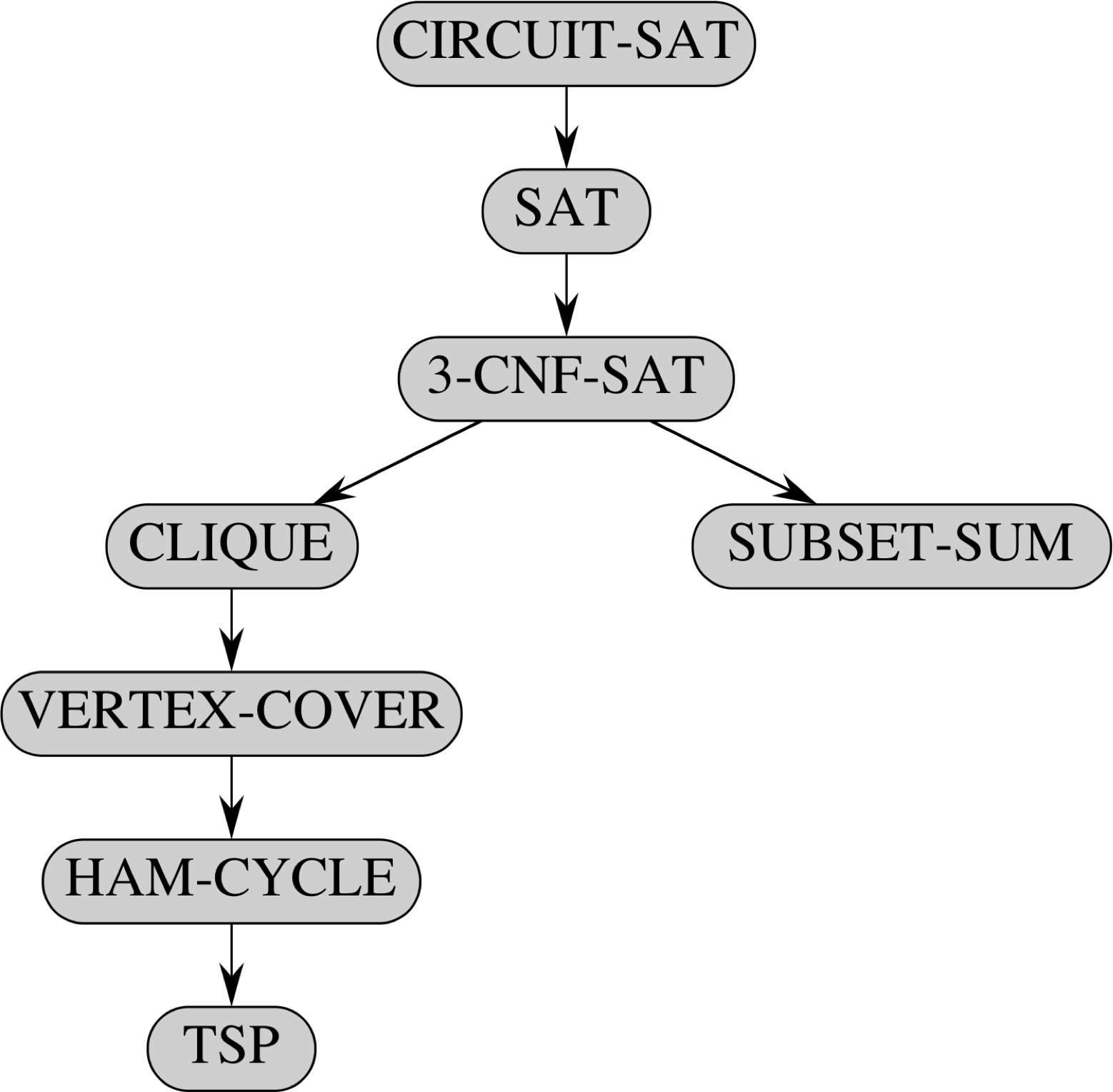
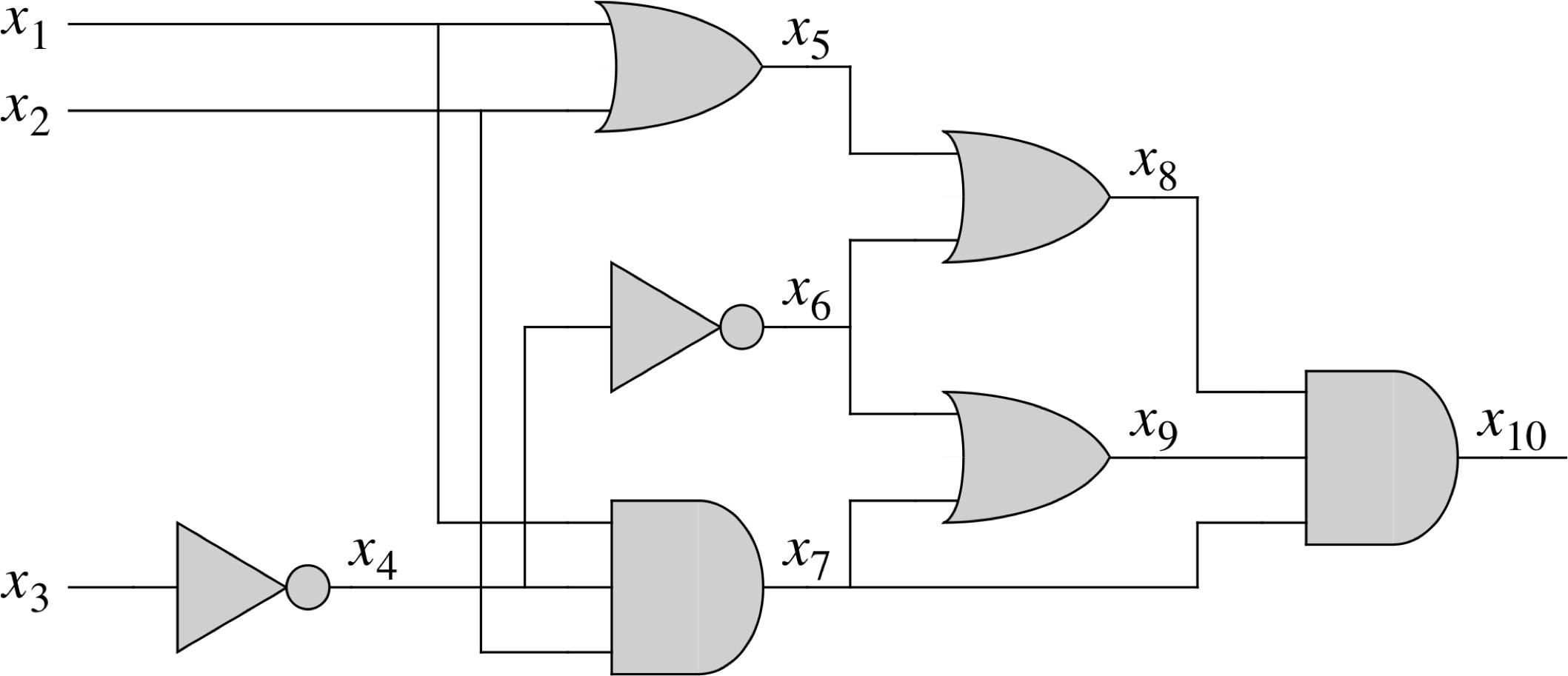
Circuit Satisfiability

Two things to prove:
- Circuit-satisfiability is in NP
- Circuit-satisfiability is NP-hard (every other problem in NP can be reduced to it)
NP-Hardness of Circuit Satisfiability
Algorithm A for some problem, PA, in NP runs in polynomial time on input x and certificate y, and produces a yes/no answer.

Circuit Satisfiability to Formula Satisfiability
Can go from SAT to 3-CNF SAT
3-CNF SAT to Clique

Some Other Well-Known NP-complete Problems
- Vertex-cover problem
- Hamiltonian-cycle problem
- Traveling-salesman problem
- Subset-sum problem
- Subgraph-isomorphism problem
- 0-1 integer-programming problem
- Integer linear-programming problem
- Independent set problem
- Graph coloring problem
Recap
B403: Introduction to Algorithm Design and Analysis
What We Did Not Cover
- B-Trees
- Fibonacci heaps
- Maximum flow / min cut
- Amortized analysis
- Sting matching
- Linear programming
What We Covered
- Fundamentals: setting up and solving recurrences, master method
- Divide and Conquer algorithms: sorting, maximum subarray, matrix multiplication
- Probabilistic analysis of randomized algorithms
- Sorting: Quicksort, n⋅log(n) lower bound, sorting in linear time, order statistics
- Data structures: Red-black trees, (hash tables), disjoint-set union-find, enhancements to red-black trees
- Dynamic programming: rod-cutting, matrix-chain multiplication, longest common subsequence, (gerrymandering)
- Greedy algorithms: activity selection, huffman coding
- Graph algorithms: minimum-spanning tree, topological sort, strongly-connected components, single-source shortest paths, (all-pair shortest paths)
- Multithreaded algorithms
- NP completeness