Multithreaded Algorithms
B403: Introduction to Algorithm Design and Analysis
Basic Terms
- Shared memory vs distributed memory
- Static vs dynamic multithreading
- Dynamic multithreading: keywords
- spawn
- sync
- parallel
P-Fib(n) 1 if n ≤ 1 2 return n 3 else spawn P-Fib(n−1) 4 y = P-Fib(n−2) 5 sync 6 return x + y
DAG Representing P-Fib
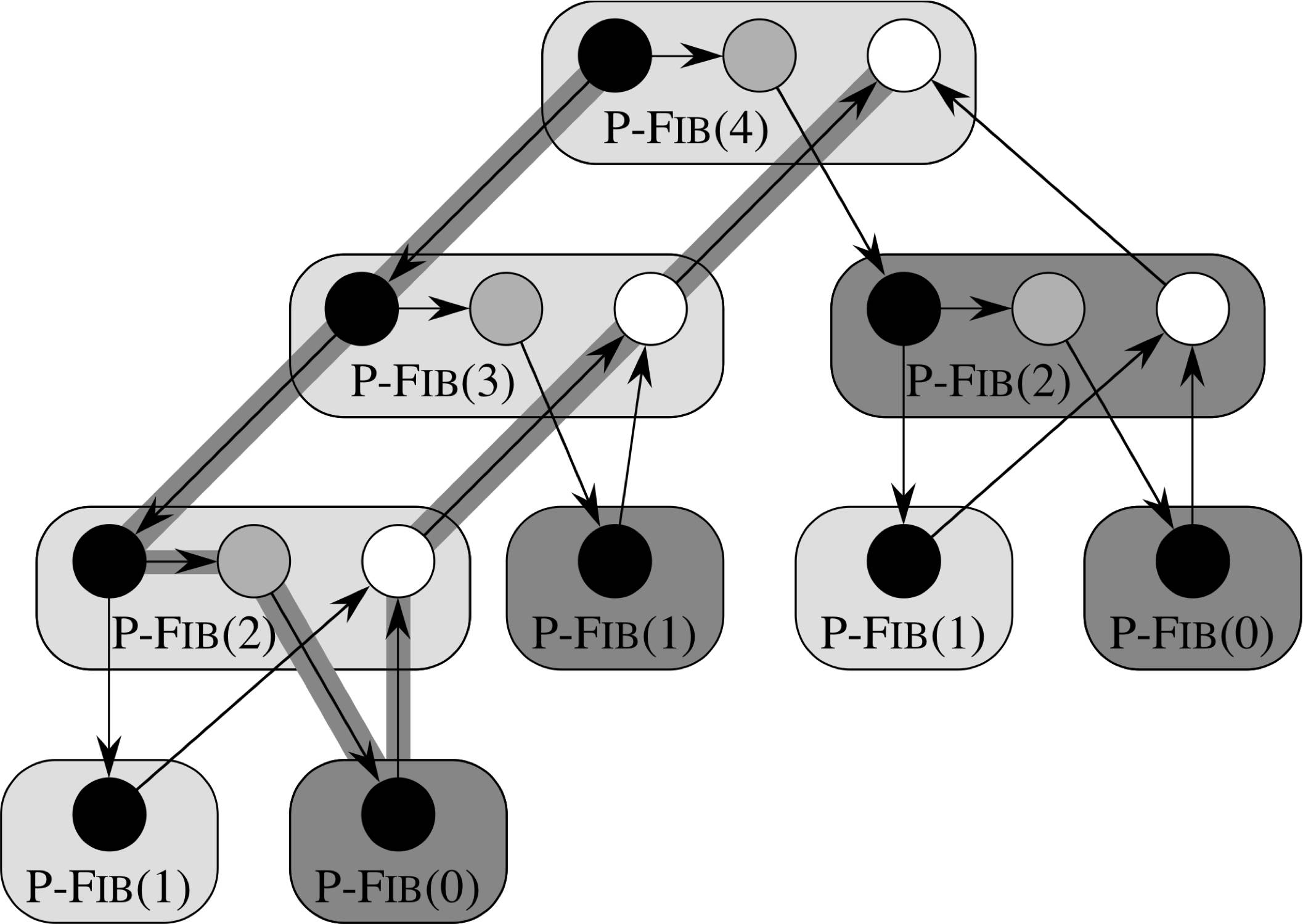
Assume Ideal Parallel Computer
- Sequential consistency
- All processors have equal processing power
- Zero overheads of memory access and task scheduling
Measuring Parallel Performance
- Work: total time to execute on one processor
- Span: Longest time to execute the strands along any path in the DAG
- Computable in O(V+E) time How?
-
T1: time on single processor
TP: time on P processors
T∞: time on unlimited number of processors - Work law: TP ≥ T1 / P
- Span law: TP ≥ T∞
- T1 / T∞ gives the parallelism
- (T1/T∞) / P = T1/(P T∞) is (parallel) slackness
Parallel Mat-Vec
Mat-Vec(A, x)
1 n = A.rows
2 let y be a new vector of length n
3 parallel for i = 1 to n
4 yi = 0
5 parallel for i = 1 to n
6 for j = 1 to n
7 yi = yi + aij⋅xj
8 return y
|
Mat-Vec-Main-Loop(A, x, y, n, i, i') 1 if i == i' 2 for j = 1 to n 3 yi = yi + aij⋅xj 4 else mid = floor((i+i')/2) 5 spawn Mat-Vec-Main-Loop(A, x, y, n, i, mid) 6 Mat-Vec-Main-Loop(A, x, y, n, mid+1, i') 7 sync |
Race Conditions
Race-Example()
1 x = 0
2 parallel for i = 1 to 2
3 x = x + 1
4 print x
Mat-Vec-Wrong()
1 n = A.rows
2 let y be a new vector of length n
3 parallel for i = 1 to n
4 yi = 0
5 parallel for i = 1 to n
6 parallel for j = 1 to n
7 yi = yi + aij⋅xj
8 return y
Parallel Matrix Multiply
P-Matrix-Multiply-Recursive(C, A, B) 1 n = A.rows 2 if n == 1 3 c11 = a11⋅b11 4 else let T be a new n×n matrix 5 partition A, B, C, and T into n/2×n/2 submatrices A11, A12, A21, A22; etc. 6 spawn P-Matrix-Multiply-Recursive(C11, A11, B11) 7 spawn P-Matrix-Multiply-Recursive(C12, A11, B12) 8 spawn P-Matrix-Multiply-Recursive(C21, A21, B11) 9 spawn P-Matrix-Multiply-Recursive(C22, A21, B12) 10 spawn P-Matrix-Multiply-Recursive(T11, A12, B21) 11 spawn P-Matrix-Multiply-Recursive(T12, A12, B22) 12 spawn P-Matrix-Multiply-Recursive(T21, A22, B21) 13 P-Matrix-Multiply-Recursive(T22, A22, B22) 14 sync 15 parallel for i = 1 to n 16 parallel for j = 1 to n 17 cij = cij + tij