Minimum Spanning Tree
B403: Introduction to Algorithm Design and Analysis
Minimum Spanning Tree
Given an undirected graph G = (V, E), and a weight function w(u,v) for each edge (u,v) ∈ E, find an acyclic subset T ⊆ E that connects all of the vertices whose total weight
w(T) = Σ(u,v)∈T w(u,v)
is minimized.
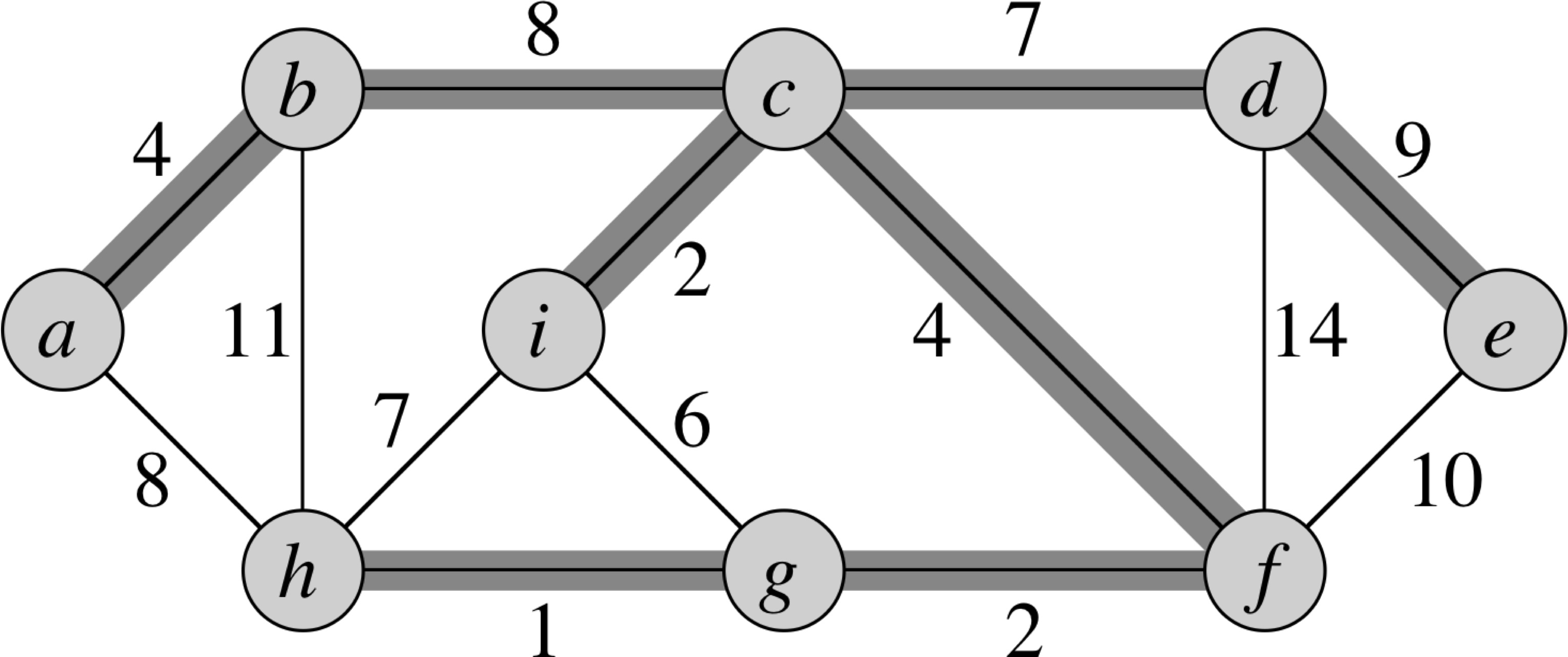
Generic MST
Generic-MST(G, w) 1 A = φ 2 while A does not form a spanning tree 3 find an edge (u,v) that is safe for A 4 A = A ∪ {(u,v)} 5 return A
Invariant: Prior to each iteration, A is a subset of some minimum spanning tree.
Definitions
Safe edge: An edge that may be added to A without violating the invariant that A is a subset of some minimum spanning tree.
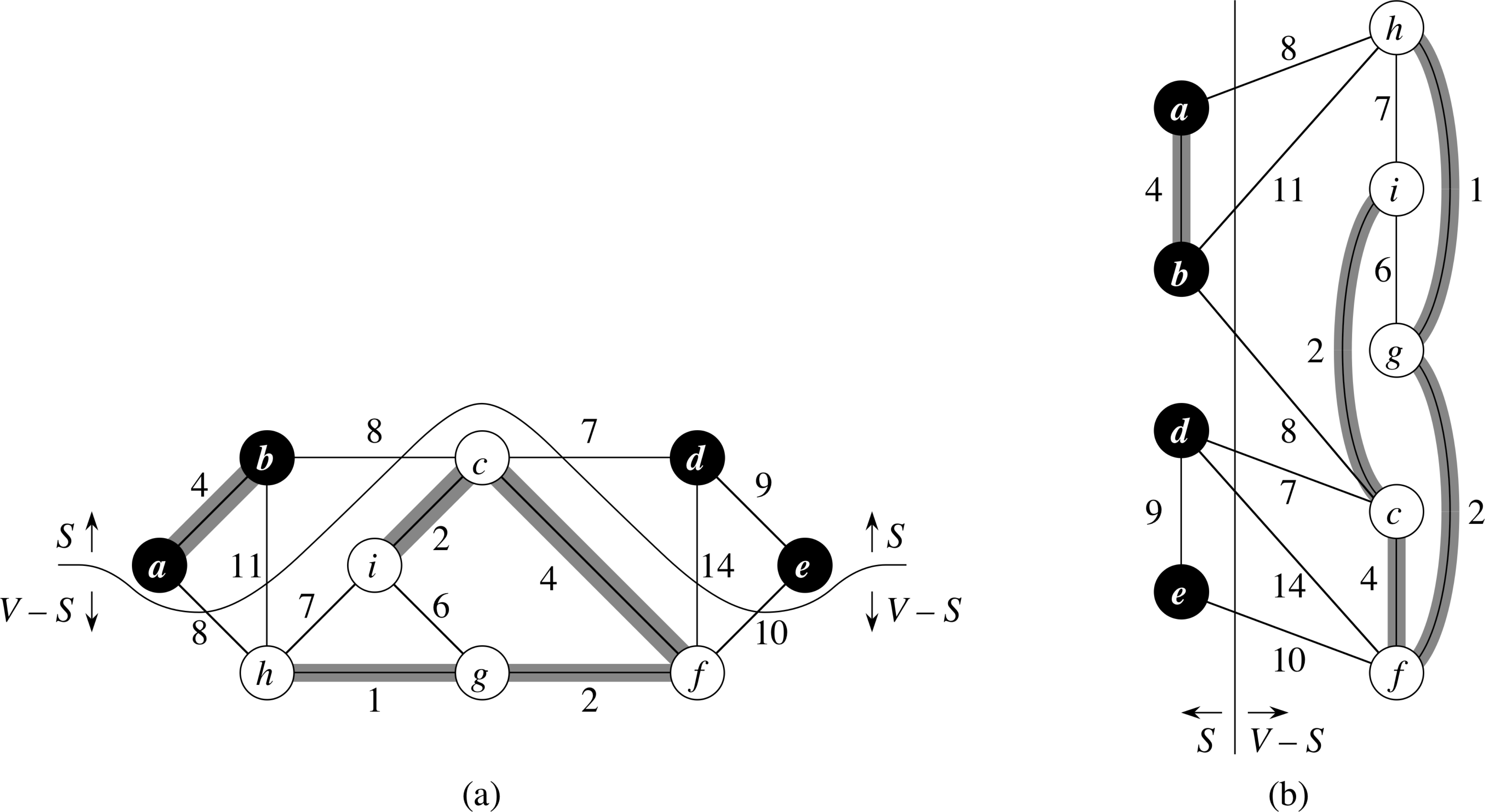
Cut: is a partition of V into S and V−S.
Crossing: An edge (u,v) ∈ E crosses the cut (S, V−S) if one of its endpoints is in S and the other is in (V−S).
Respecting: A cut respects a set A of edges if no edge in A crosses the cut.
Light edge: An edge is a light edge crossing a cut if its weight is the minimum of any edge crossing the cut. Note that there may be more than one light edge.
Cut Example
Theorem
Theorem Let G = (V, E) be a connected, undirected graph with a real-valued weight function w defined on E. Let A be a subset of E that is included in some minimum spanning tree for G, let (S, V−S) be any cut of G that respects A, and let (u,v) be a light edge crossing (S, V−S). Then edge (u, v) is safe for A.
Proof
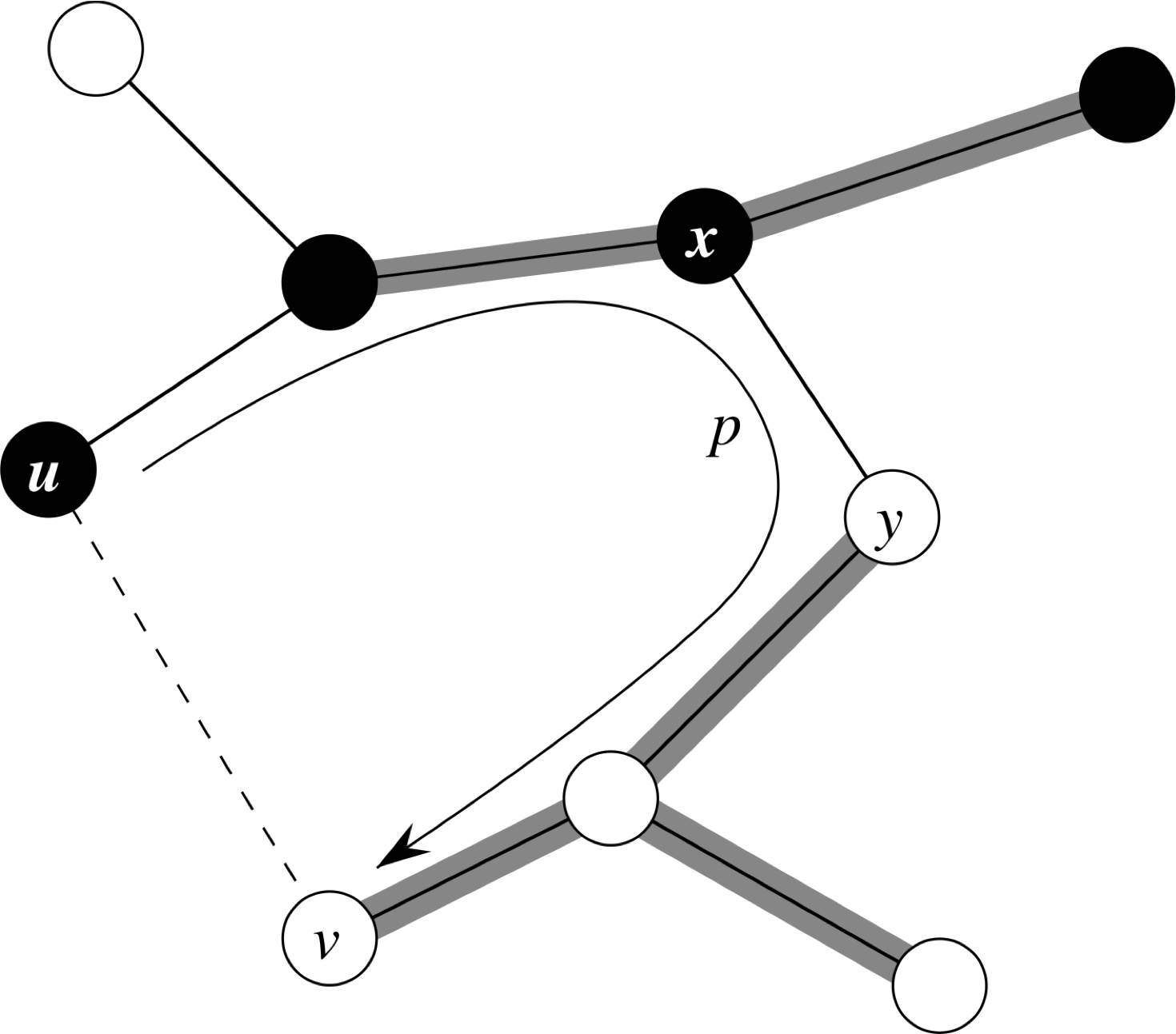
Claims / Questions
- A minimum weight edge in an undirected graph belongs to some minimum spanning tree.
- The inverse of the Theorem about safe edges is not true. In other words, if (u,v) is a safe edge for A crossing (S, V−S) then it is not necessarily a light edge.
Consider the set:
{(u,v) : there exists a cut (S, V−S) such that (u,v) is a light edge crossing it}
Does this set form a minimum spanning tree?
- If e is a maximum-weight edge on some cycle of connected graph G = (V, E), then there is a minimum spanning tree of G that does not include e.
- If we decrease the weight of an edge in the minimum spanning tree T of a graph, then T is still a minimum spanning tree.
- Follows directly from the Theorem about safe edges.
- Consider the graph: G = (V,E), V = {a, b, c}, E = {a-b, a-c, b-c} and the weight function w: {w(a-b) = 1, w(a-c) = 2, w(b-c) = 2}. Suppose that we start the greedy algorithm at a, thus S = {a}. The greedy algorithm will always start by picking the light edge a-b. However, a-c is also a safe edge to pick. Thus, even though a-c is a safe edge, it is not light.
- This is an overly inclusive set. Consider a graph G = (V,E), V = {a, b, c}, E = {a-b, a-c, b-c} and the weight function w: {w(a-b) = w(a-b) = w(b-c) = 1}. Each edge is a light edge of some cut. However, all three edges together do not form a tree.
- We can use a “cut-and-paste” argument, the kind we have used in proving greedy properties of problems. If e is not a part of the MST then we are done. If it is, then consider a cycle that it is part of (according to the assumption it is a part of at least one cycle). There must be at least one edge (u,v) on this cycle that is not a part of the MST. Remove e from the MST and add (u,v) to it. The resulting graph still have no cycles, so it continues to be a tree; it still covers all vertices, so it is a spanning tree; and its weight doesn't go up, so it is still a minimum spanning tree. Thus, given an MST with e in it, we can construct one without e.
- This follows almost trivially, since by decreasing an edge weight the total weight of the MST only goes down, and there can be no other smaller weight spanning tree.
Prim's Algorithm
MST-Prim (G, w, r) 1 for each u ∈ G.V 2 u.key = ∞ 3 u.π = NIL 4 r.key = 0 5 Q = G.V 6 while Q ≠ φ 7 y = Extract-Min(Q) 8 for each v ∈ G.Adj[u] 9 if v ∈ Q and w(u,v) < v.key 10 v.π = u 11 v.key = w(u,v)
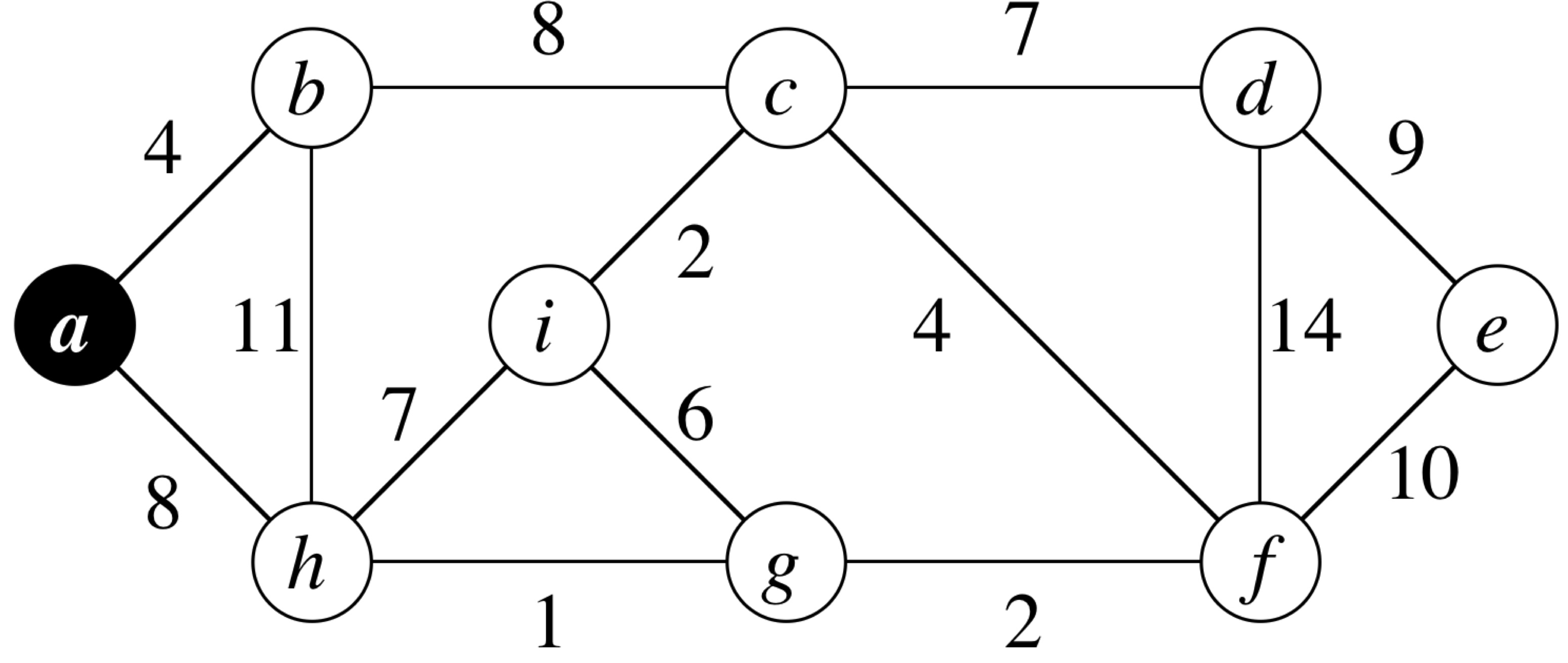

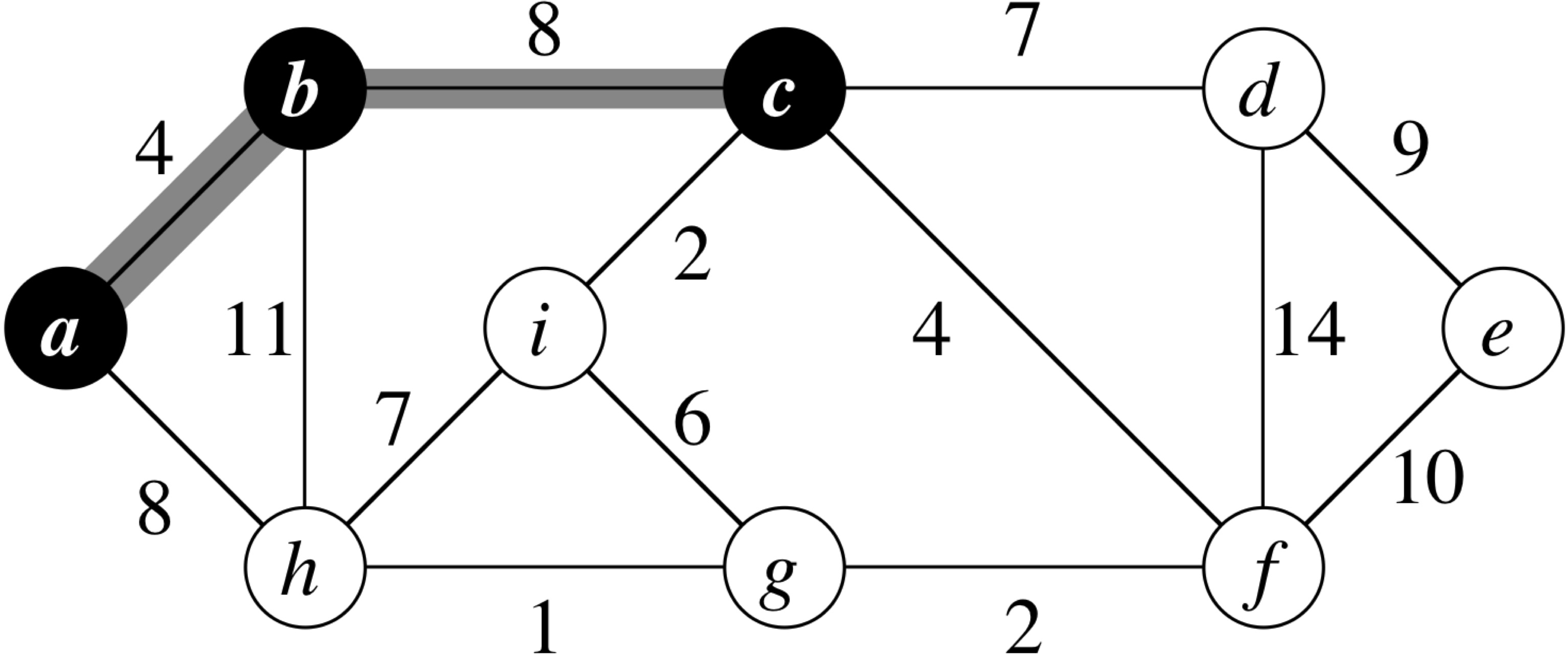
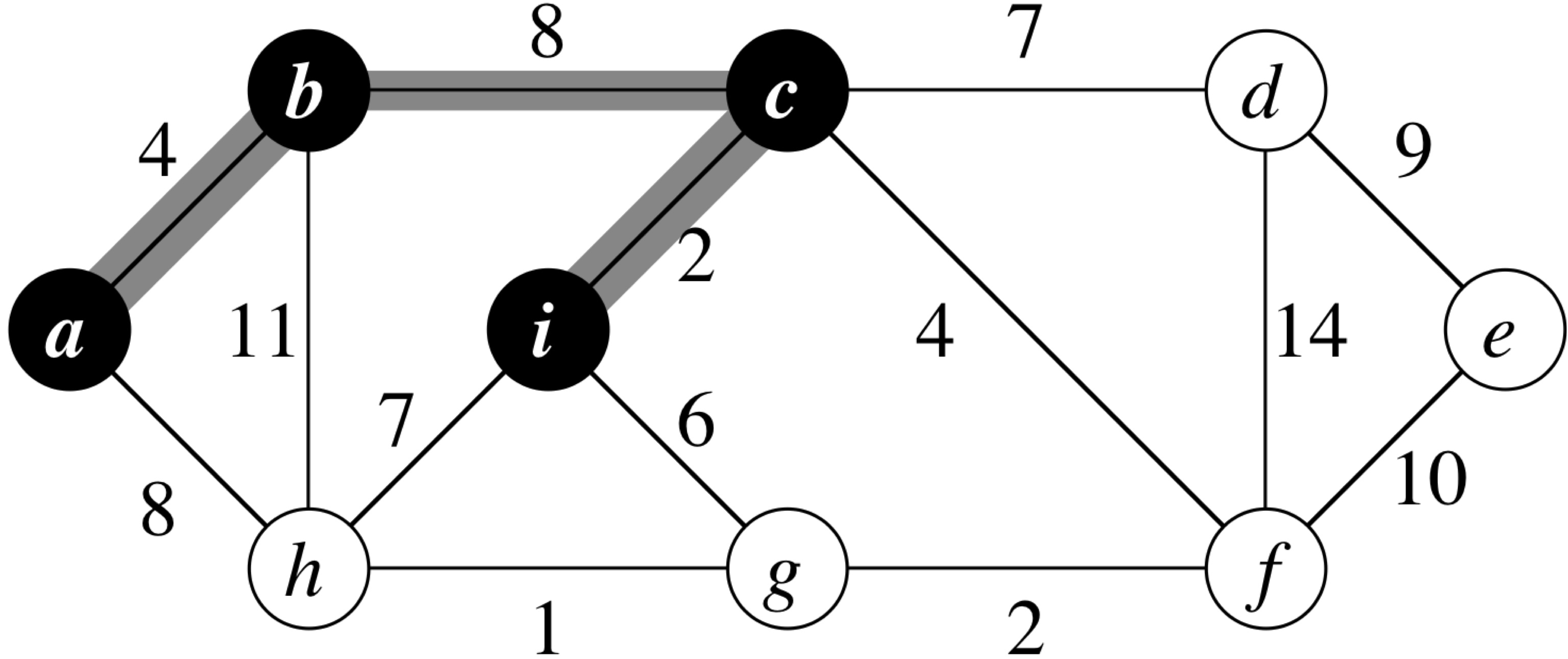
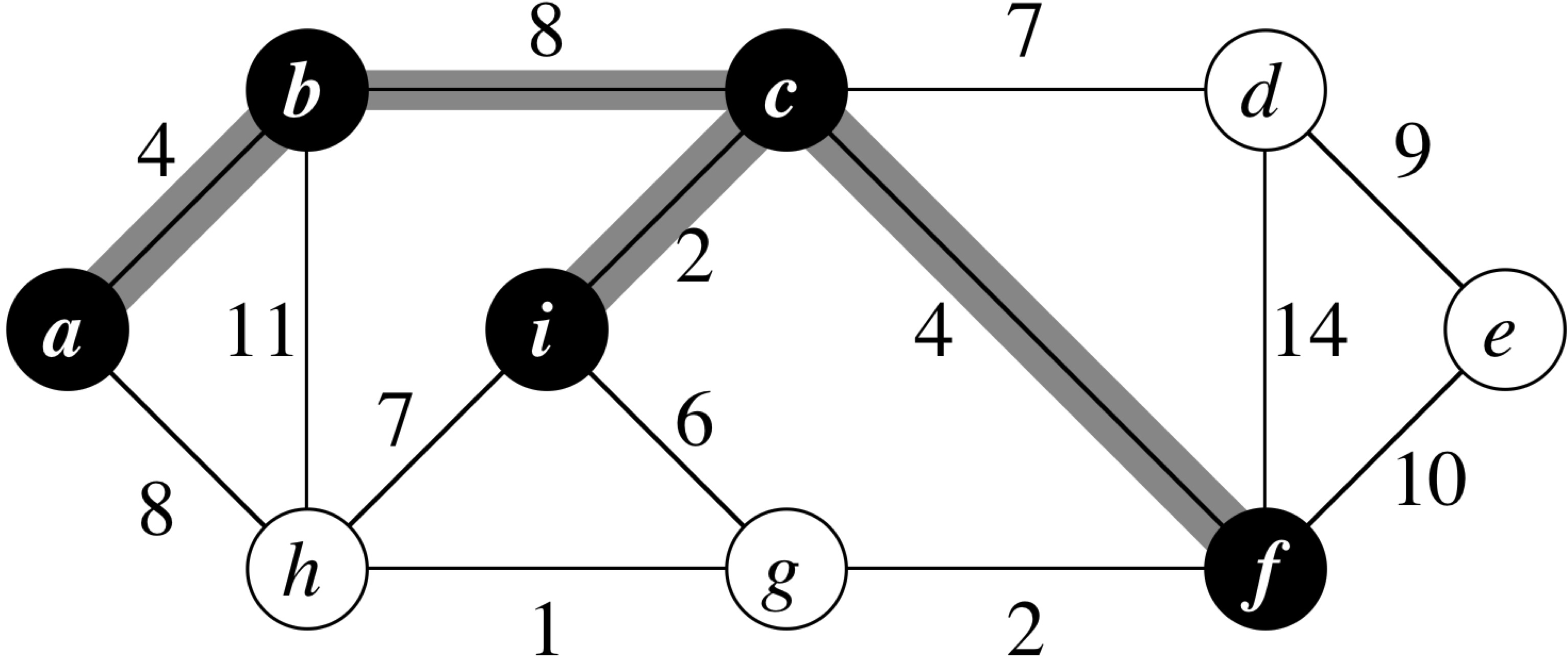
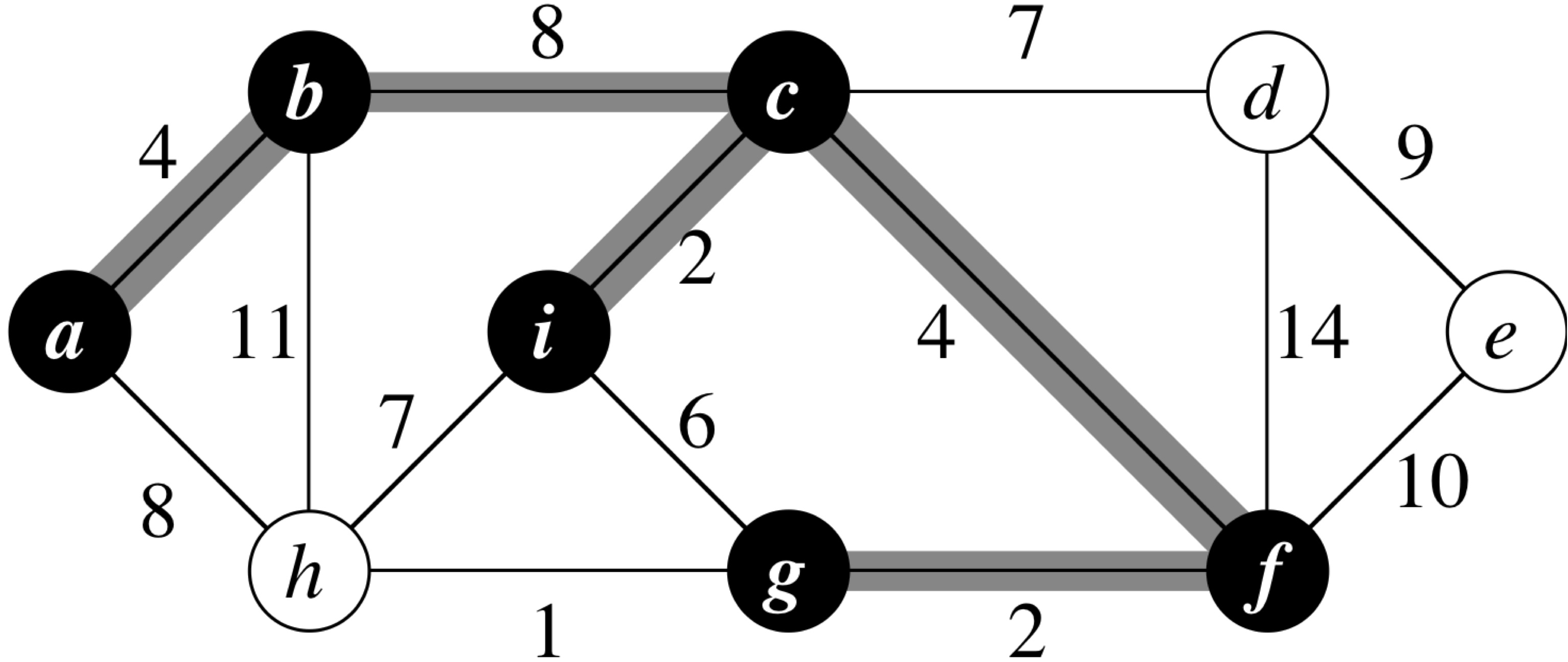


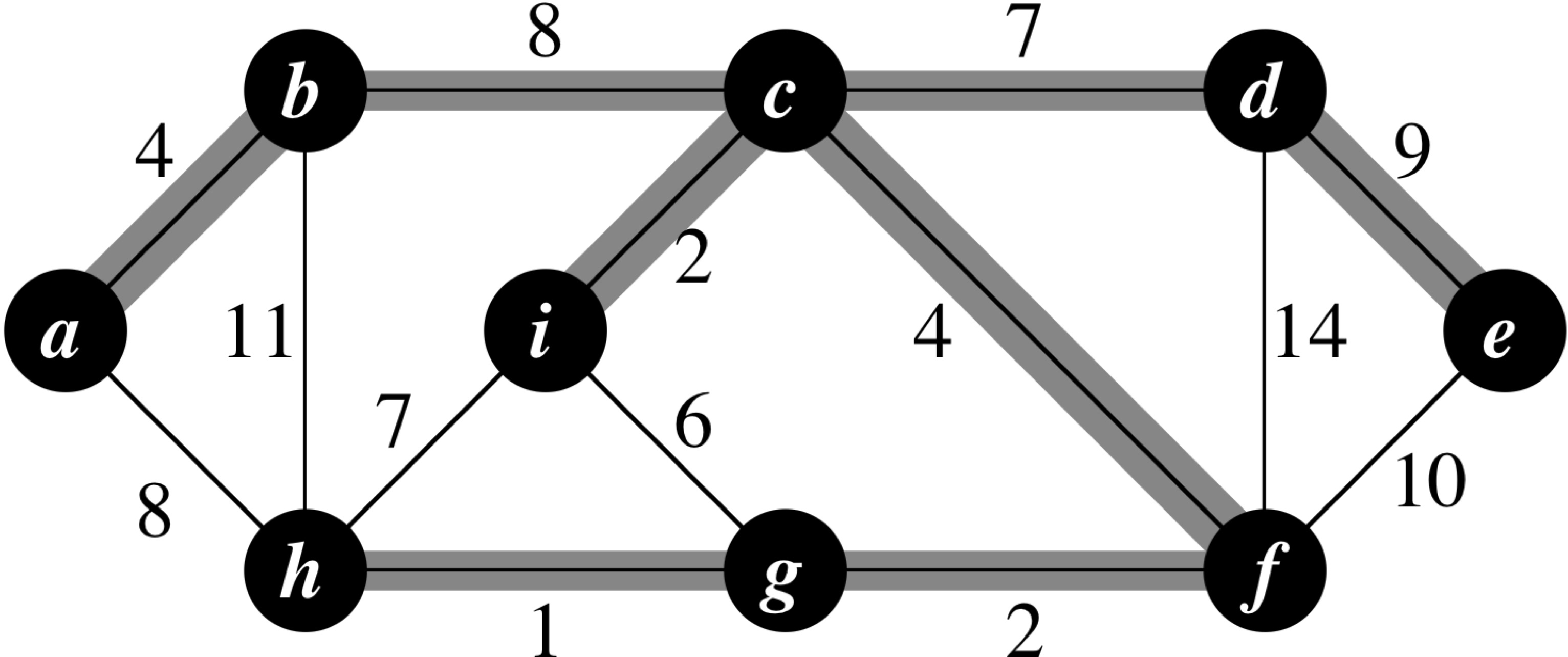
Prim's Algorithm: Running Time
MST-Prim (G, w, r) 1 for each u ∈ G.V 2 u.key = ∞ 3 u.π = NIL 4 r.key = 0 5 Q = G.V 6 while Q ≠ φ 7 y = Extract-Min(Q) 8 for each v ∈ G.Adj[u] 9 if v ∈ Q and w(u,v) < v.key 10 v.π = u 11 v.key = w(u,v)
- Implement Q as a min-priority queue (logarithmic Extract-Min and Decrease-Key operations)
- Lines 1-5 in log(V) time, using Build-Min-Heap
- Body of the while-loop executes |V| times, leading to a total time of O(V log(V)) for all calls to Extract-Min
- The for-loop in line 8 executes a total of 2×|E| times, leading to a running time of O(E log(V)) across all invocations of the for-loop
Total running time = O(V log(V) + E log(V)) = O(E log(V))
Union-Find Data Structure for Disjoint Sets
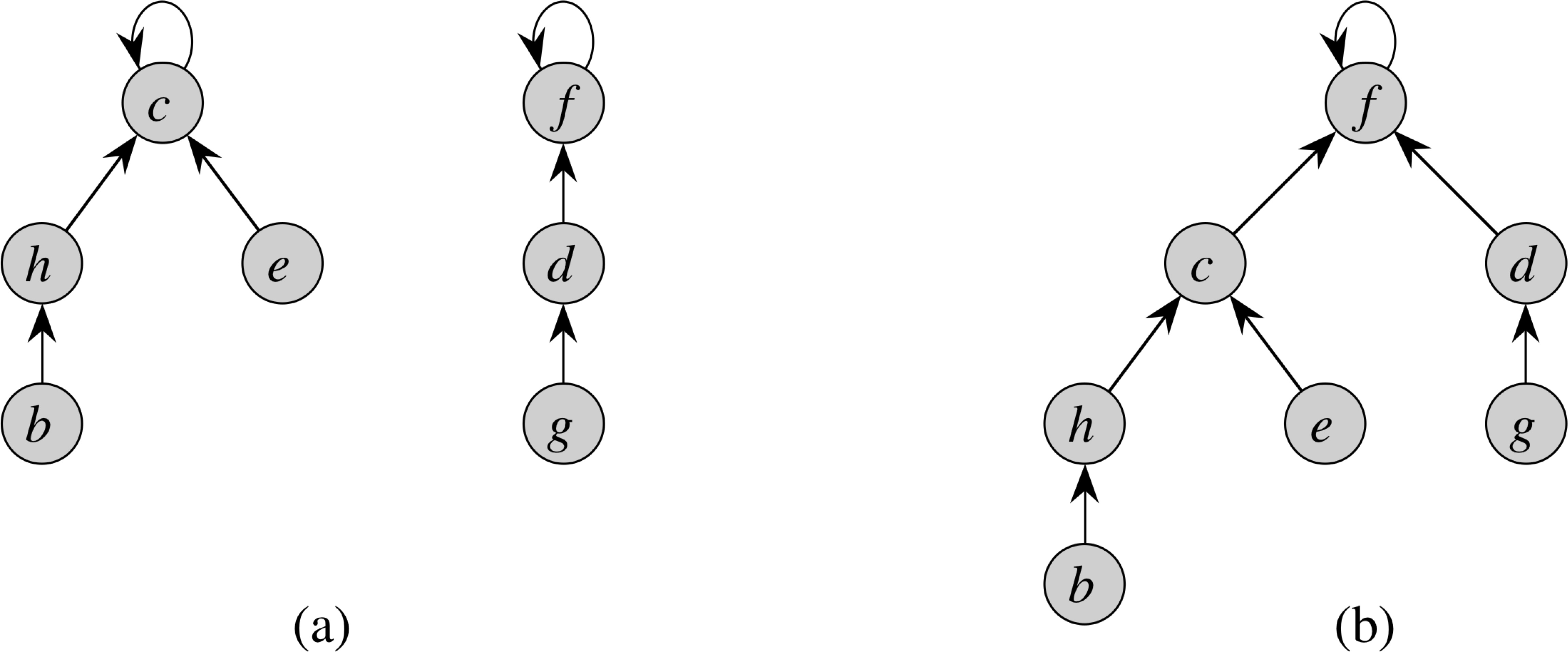
Union-Find Data Structure for Disjoint Sets
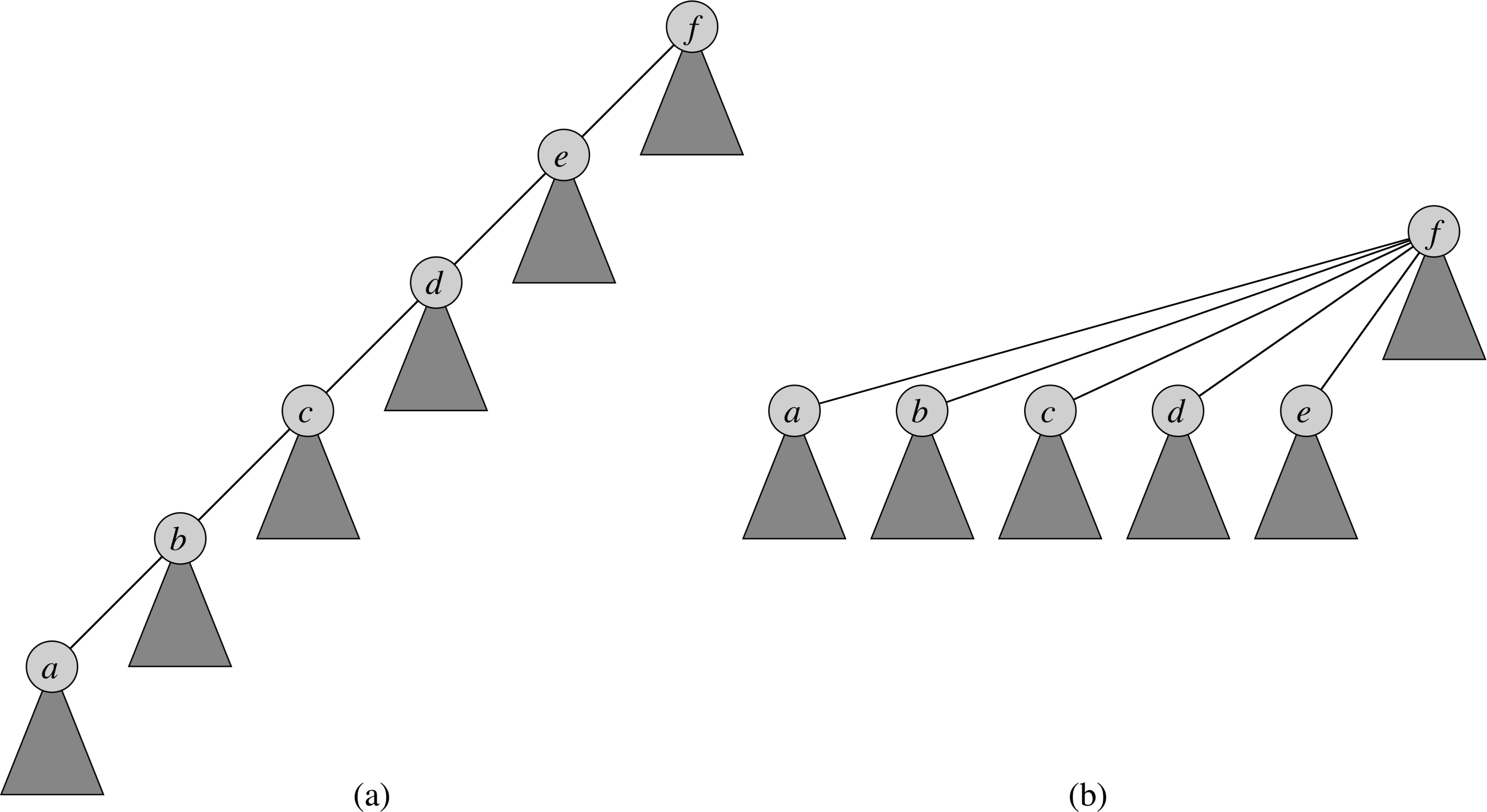
Union-Find Algorithm
Make-Set(x)
1 x.p = x
2 x.rank = 0
Union(x, y) 1 Link(Find-Set(x), Find-Set(y))
Link(x, y)
1 if x.rank > y.rank
2 y.p = x
3 else
x.p = y
4 if x.rank == y.rank
5 y.rank = y.rank + 1
Find-Set(x) 1 if x ≠ x.p 2 x.p = Find-Set(x.p) 3 return x.p
Running Time
Kruskal's Algorithm
MST-Kruskal 1 A = φ 2 for each vertex v ∈ G.V 3 Make-Set(v) 4 sort the edges of G.E into nondecreasing order by weight w 5 for each edge (u,v) ∈ G.E, taken in nondecreasing order by weight 6 if Find-Set(u) ≠ Find-Set(v) 7 A = A ∪ {(u,v)} 8 Union(u,v) 9 return A
Running time = O(E⋅log(V)), using union-find data structure for disjoint sets, with path compression