Greedy Algorithms
B403: Introduction to Algorithm Design and Analysis
Activity Selection Problem
We are given a set S = {a1, a2, ..., an} of n proposed activities that wish to use a resource that only one activity can use at a time. Each activity ai has a start time si and a finish time fi, where 0 ≤ si ≤ fi ≤ ∞. Activity ai takes place in the half-open time interval [si, fi). Activities ai and aj are compatible if the intervals [si, fi) and [sj, fj) do not overlap, i.e., if si ≥ fk or sj ≥ fi.
Activity Selection Problem: Select a maximum-size subset of mutually compatible activities, assuming that the activities are sorted in monotonically increasing order of finish time:
f1 ≤ f2 ≤ ... ≤ fn
Greedy Choice Property
Let Sk = {ai ∈ S : si ≥ fk} be the set of activities that start after ak finishes.
Theorem Consider any nonempty subproblem Sk, and let am be an activity in Sk with the earliest finish time. Then am is included in some maximum-size subset of mutually compatible activities of Sk.
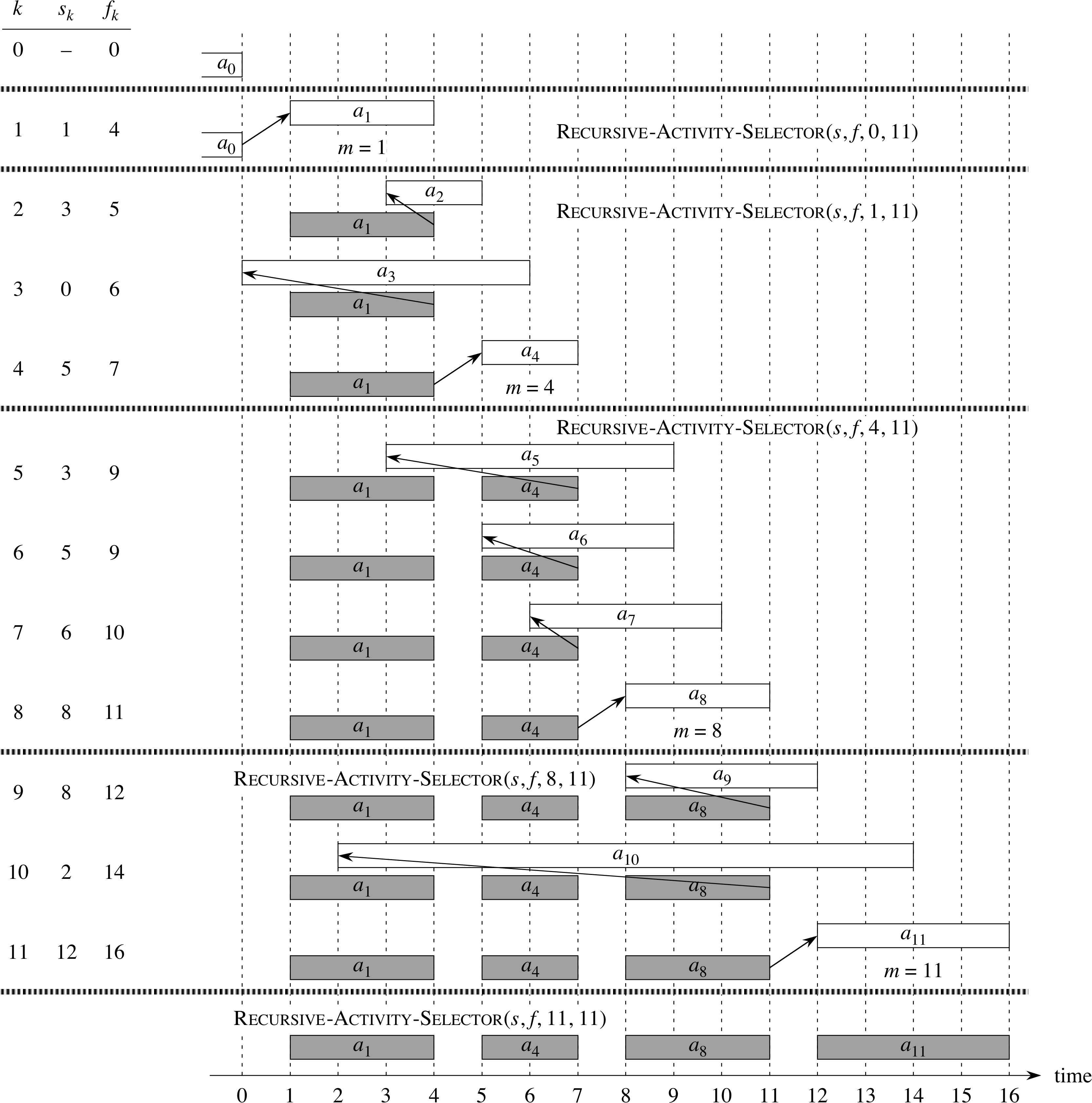
Example for Recursive Algorithm
Elements of the Greedy Strategy
- Determine the optimal substructure of the problem
- Develop a recursive solution
- Show that if we make the greedy choice, then only one subproblem remains
- Prove that it is always safe to make the greedy choice
- Develop a recursive algorithm that implements the greedy strategy
- Convert the recursive algorithm to an iterative one
Simplified Elements of the Greedy Strategy
- Cast the optimization problem as one in which we make a choice and are left wit one subproblem to solve
- Prove that there is always an optimal solution to the original problem that makes the greedy choice, so that the greedy choice is always safe
- Demonstrate optimal substructure by showing that an optimal solution can be obtained by combining the greedy choice with the solution to the one subproblem remaining after making the greedy choice
Dynamic Programming vs Greedy Strategy
- Choice
- Dynamic programming depends on the solutions to the subproblems to make a choice, greedy strategy makes a choice without looking at the subproblems
- Order of solving subproblems
- Bottom-up in dynamic programming (usually) vs top-down in greedy
- Applicability
- Greedy strategy is usually applicable only to a subset of problems that could be solved using dynamic programming
- Efficiency
- Whenever applicable, greedy strategy is more efficient than dynamic programming because it looks at fewer choices
Fractional vs 0/1 Knapsack

Huffman Coding

Prefix Codes: Each code has a unique prefix
What is desirable about prefix codes?
Trees for the Two Coding Schemes

Example of Huffman Coding Algorithm

Correctness of Huffman Coding Algorithm
Lemma Let C be an alphabet in which each character c ∈ C has frequency c.freq. Let x and y be two characters in C having the lowest frequencies. Then there exists an optimal prefix code for C in which the codewords for x and y have the same length and differ only in the last bit.
Proof

Correctness of Huffman Coding Algorithm
Lemma Let C be a given alphabet with frequency c.freq defined for each character c ∈ C. Let x and y be two characters in C with minimum frequency. Let C' be the alphabet C with the characters x and y removed and a new character z added, so that C' = C − {x, y} ∪ {z}. Define f for C' as for C, except that z.freq = x.freq + y.freq. Let T' be any tree representing an optimal prefix code for the alphabet C'. Then the tree T, obtained from T' by replacing the leaf node for z with an internal node having x and y as children, represents and optimal prefix code for the alphabet C.
Claims and Questions
- A binary tree that is not full cannot correspond to an optimal prefix code.
- What is an optimal Huffman code when the frequencies are the first n Fibonacci numbers?
- If we order the characters in an alphabet so that their frequencies are monotonically decreasing, then there exists an optimal code whose codeword lengths are monotonically increasing.
- No compression scheme can expect to compress a file of randomly chosen 8-bit characters by even a single bit.