Dynamic Programming
B403: Introduction to Algorithm Design and Analysis
Rod-Cutting Example
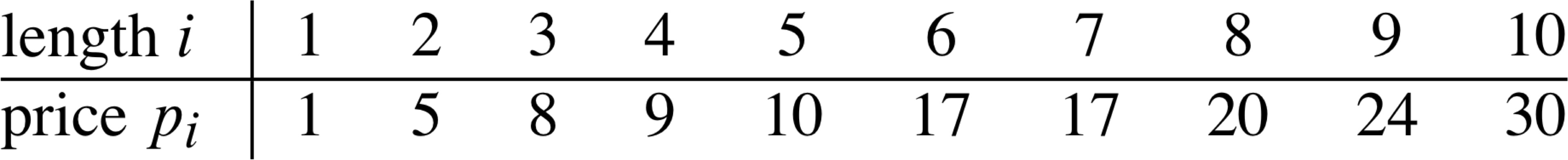

Cut-Rod
Cut-Rod (p, n) 1 if n == 0 2 return 0 3 q = −∞ 4 for i = 1 to n 5 q = max (q, p[i] + Cut-Rod(p,n−i)) 6 return q
Rod-Cutting Recursion Tree

Memoized Cut-Rod
Memoized-Cut-Rod (p, n) 1 let r[0..n] be a new array 2 for i = 0 to n 3 r[i] = −∞ 4 return Memoized-Cut-Rod-Aux(p, n, r)
Memoized-Cut-Rod-Aux (p, n, r) 1 if r[n] ≥ 0 2 return r[n] 3 if n == 0 4 q = 0 5 else q = −∞ 6 for i = 1 to n 7 q = max(q, p[i] + Memoized-Cut-Rod-Aux(p, n−i, r)) 9 r[n] = 1 10 return q
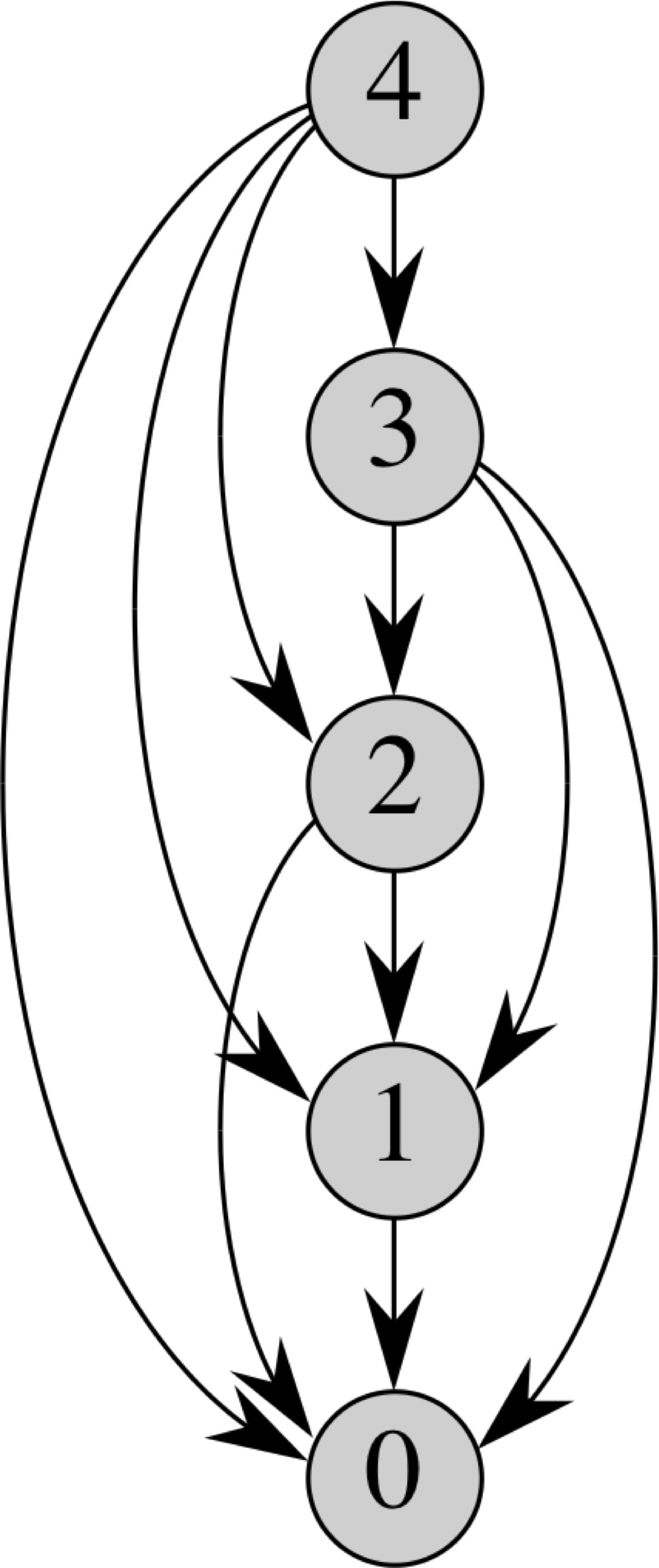
Bottom Up Cut-Rod
Bottom-Up-Cut-Rod (p, n)
1 let r[0..n] be a new array
2 r[0] = 0
3 for j = 1 to n
4 q = −∞
5 for i = 1 to j
6 q = max(q, p[i] + r[j−i])
7 r[j] = q
4 return r[n]
Rod-Cutting Subproblem Graph
Matrix-chain Multiplication
Problem: Find optimal parenthesization for multiplying a chain of matrices:
A1 A2 ... An
Key observations:
- Matrix multiplication is associative
- The cost of multiplying two matrices of sizes p×q and q×r is p⋅q⋅r
- The cost of multiplying a matrix chain can vary dramatically depending on parenthesization
Many Ways to Parenthesize
|
For n = 4
|
Matrix-Multiply (A, B)
1 if A.columns ≠ B.rows
2 error "incompatible dimensions"
3 else
let C be a new A.rows × B.columns matrix
4 for i = 1 to A.rows
5 for j = 1 to B.columns
6 cij = 0
7 for k = 1 to A.columns
8 cij = cij + aik⋅bkj
|
Number of ways to Parenthesize
| P(n) = { | 1 | if n = 1 |
| Σ k=1 n−1 P(k)⋅P(n−k) | if n > 1 |
P(n) = Ω(2n)
Proof:
Induction step: Given that P(n) ≥ an, we can prove that P(n+1) ≥ an+1.
| P(n+1) | = | Σ n−1 k=1 P(k)⋅P(n−k) |
| ≥ | Σ n−1 k=1 ak⋅an-k | |
| = | Σ n−1 k=1 an | |
| = | n⋅an | |
| ≥ | an+1, if n ≥ a |
Base Case?

Base Case?

MATLAB Code
function count = matchainparen (n)
if (n < 1)
count = 0;
else
p = zeros(n,1);
p(1) = 1;
for i = 2:n
p(i) = 0;
for k = 1:i-1
p(i) = p(i) + p(k)*p(i-k);
end
end
count = p(n);
end
Matrix Chain Order
Matrix-Chain-Order (p)
1 n = p.length − 1
2 let m[1..n,1..n] and s[1..n,1..n] be new tables
3 for i = 1 to n
4 m[i,i] = 0
5 for l = 2 to n // l is the chain length
6 for i = 1 to n−l+1
7 j = i+l−1
8 m[i,j] = ∞
9 for k = i to j−1
10 q = m[i,k] + m[k+1,j] + pi−1⋅pk⋅pj
11 if q < m[i,j]
12 m[i,j] = q
13 s[i,j] = k
14 return m and s
Matrix Chain Multiplication Example

| matrix | A1 | A2 | A3 | A4 | A5 | A6 |
|---|---|---|---|---|---|---|
| dimension | 30×35 | 35×15 | 15×5 | 5×10 | 10×20 | 20×25 |
Constructing an Optimal Solution
Print-Optimal-Parens (s, i, j) 1 if i == j 2 print "A" 3 else print "(" 4 Print-Optimal-Parens(s, i, s[i,j]) 5 Print-Optimal-Parens(s, s[i,j]+1, j) 6 print ")"
Longest Common Subsequence (LCS) Problem
Given two sequences X = ⟨x1, x2, ..., xm⟩ and Y = ⟨y1, y2, ..., yn⟩ find a maximum length common subsequence of X and Y
Given a sequence X = ⟨x1, x2, ..., xm⟩, another sequence Z = ⟨z1, z2, ..., zk⟩ is a subsequence of X if there exists a strictly increasing sequence ⟨i1, i2, ..., ik⟩ of indices of X such that for all j = 1, 2, ..., k, we have xij = zj.
Given two sequences X and Y, we say that a sequence Z is a common subsequence of X and Y if Z is a subsequence of both X and Y.
Given a sequence X = ⟨x1, x2, ..., xm⟩, we define the ith prefix of X, for i = 0, 1, ..., m, as Xi = ⟨x1, x2, ..., xi⟩. X0 is the empty sequence.
Optimal Substructure
Theorem (Optimal substructure of an LCS)
Let X = ⟨x1, x2, ...,
xm⟩ and Y = ⟨y1, y2, ..., yn⟩ be sequences, and
let Z = ⟨z1, z2, ..., zk⟩ be any LCS of X and Y.
- If xm = yn, then zk = xm = yn, and Zk−1 is an LCS of Xm−1 and Yn−1.
- If xm ≠ yn, then zk ≠ xm implies that Z is an LCS of Xm−1 and Y.
- If xm ≠ yn, then zk ≠ yn implies that Z is an LCS of X and Yn−1.
Proof:
Case 1: If xk ≠ xm, we could add xm = yn to Z and get a longer common subsequence. Similarly, Zk−1 must be an LCS of Xm−1 and Yn−1, otherwise, we could cut-and-paste a longer subsequence to get a subsequence longer than Z.
Case 2: If zk ≠ xm then Z is be a common subsequence of Xm−1 and Y. Z must be an LCS, otherwise, if there is a longer subsequence W then it is also a longer subsequence of X and Y.
Case 3: Symmetric to case 2.
Recursive Solution
Let c[i, j] be the length of an LCS of the sequences Xi and Yj.
| T(n) = | 0 | if i = 0 or j = 0, | |
| c[i−1, j−1] + 1 | if i, j > 0 and xi = yj | ||
| max(c[i, j−1], c[i−1,j]) | if i, j > 0 and xi ≠ yj |
How long would a naïve version take?
How many distinct subproblems are there?
LCS Length
LCS-Length(X, Y)
1 m = X.length
2 n = Y.length
3 let b[1..m, 1..n] and c[0..m, 0..n] be new tables
4 for i = 1 to m
5 c[i, 0] = 0
6 for j = 0 to n
7 c[0, j] = 0
8 for i = 1 to m
9 for j = 1 to n
10 if xi == yj
11 c[i,j] = c[i−1,j−1] + 1
12 b[i,j] = “↖”
13 elseif c[i−1,j] ≥ c[i,j−1]
14 c[i,j] = c[i−1,j]
15 b[i,j] = “↑”
16 else c[i,j] = c[i,j−1]
17 b[i,j] = “←”
18 return c and b
What is the running time?
LCS Example
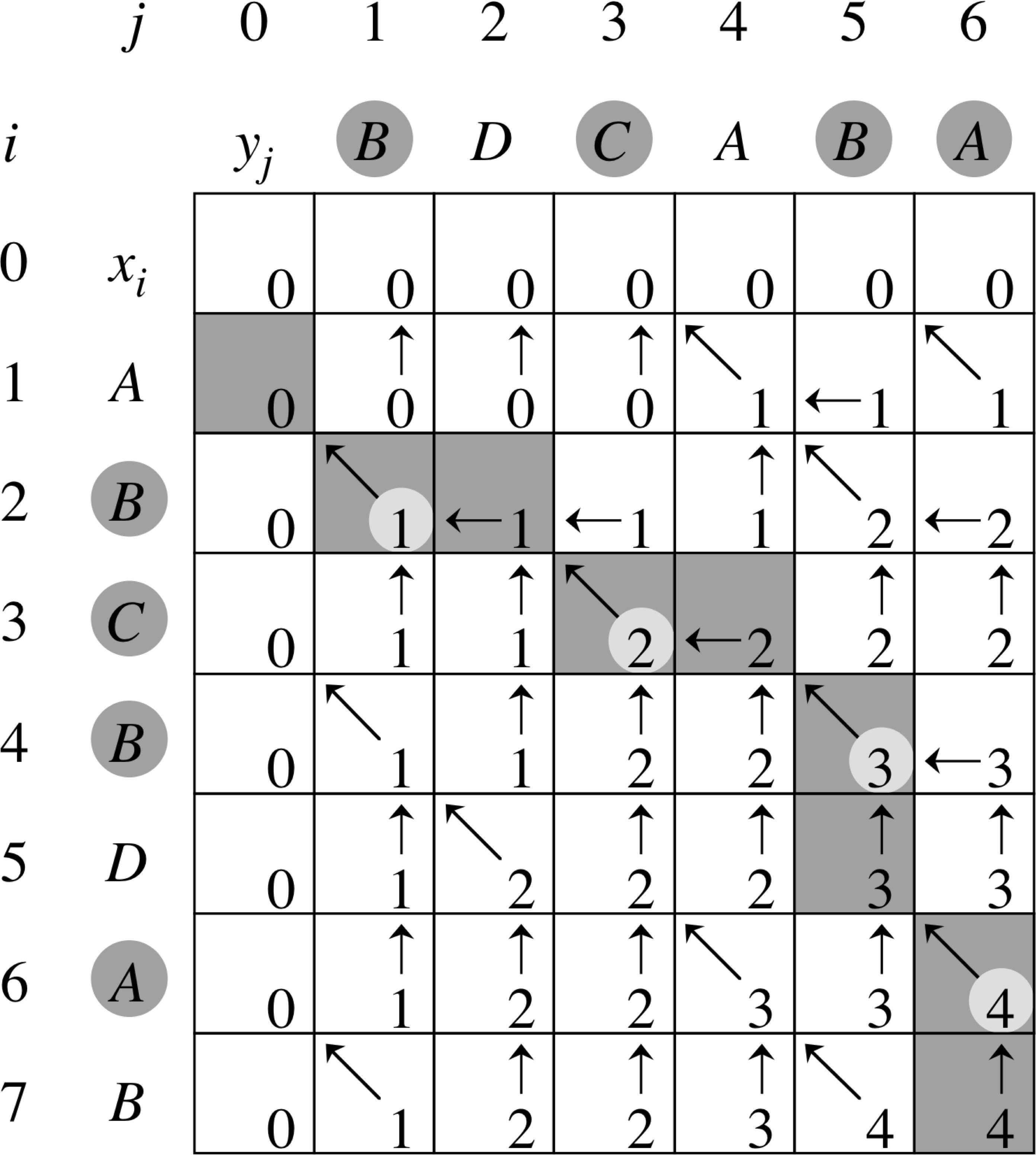
Print LCS
Print-LCS (b, X, i, j) 1 if i == 0 or j == 0 2 return 3 if b[i,j] == “↖” 4 Print-LCS(b, X, i−1, j−1) 5 print xi 6 elseif b[i,j] == “↑“ 7 Print-LCS(b, X, i−1, j) 8 else Print-LCS(b, X, i, j−1)