Red-Black Trees

Red-Black Tree Example

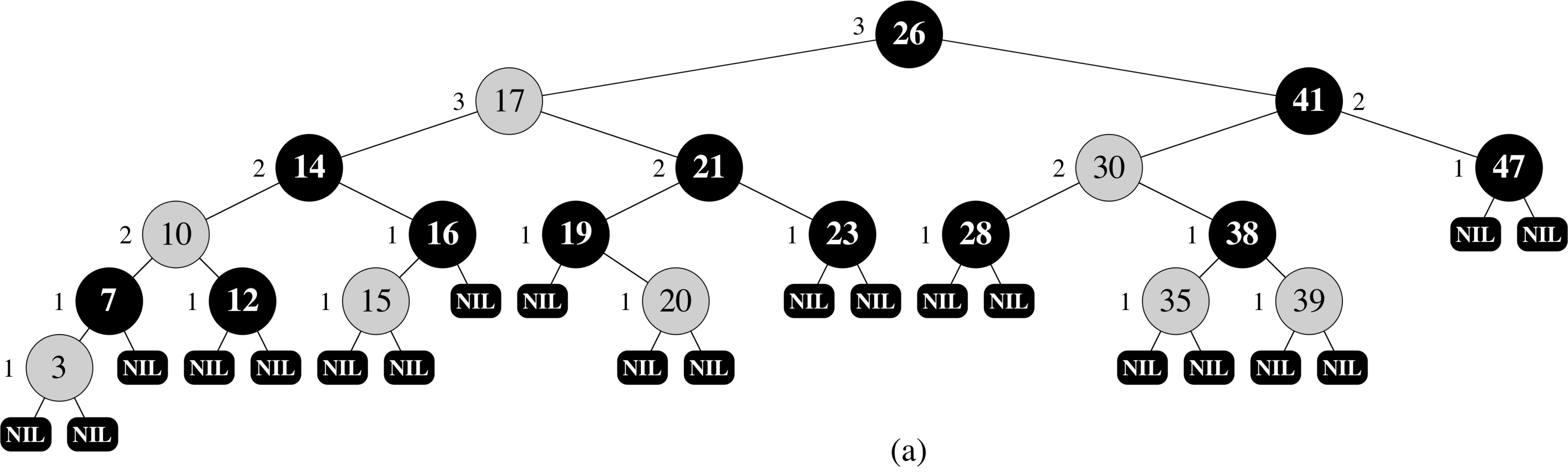
Red-Black Tree Example (internal)

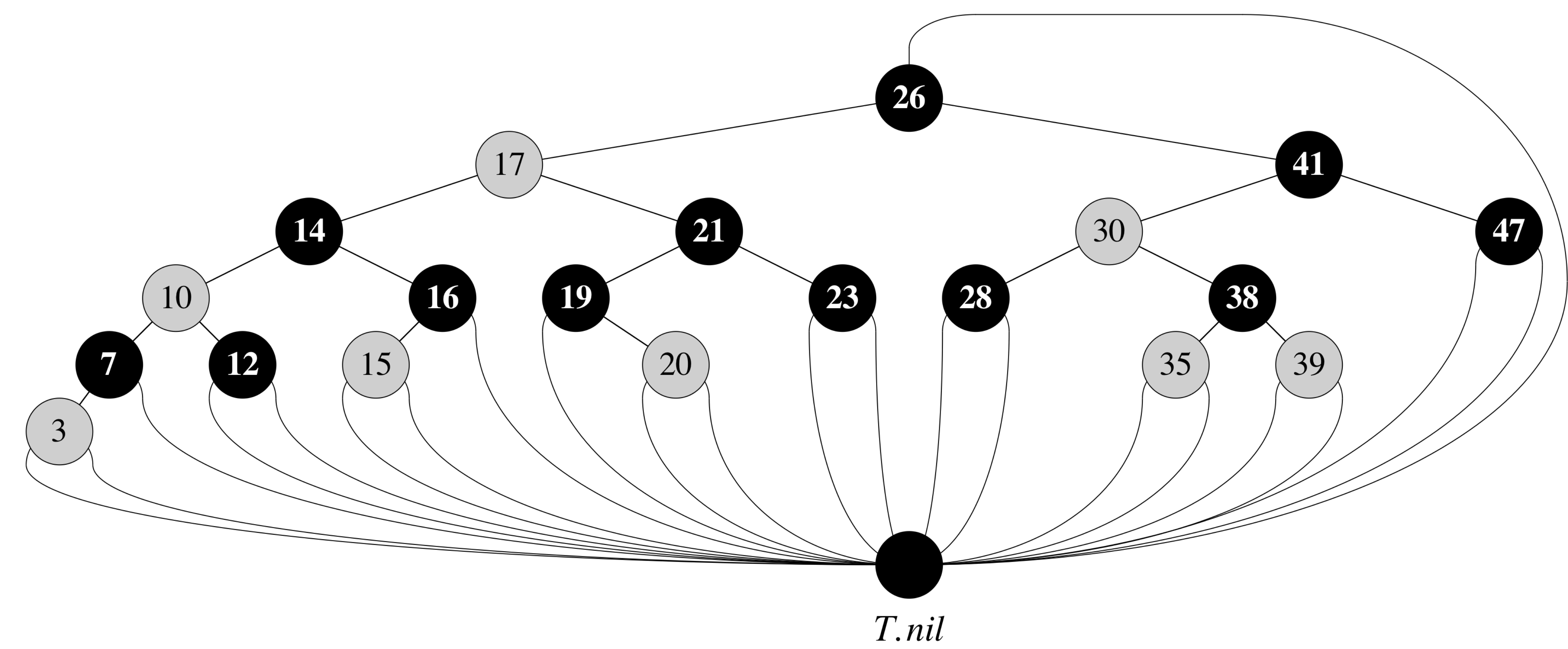
Red-Black Tree Example (simplified)

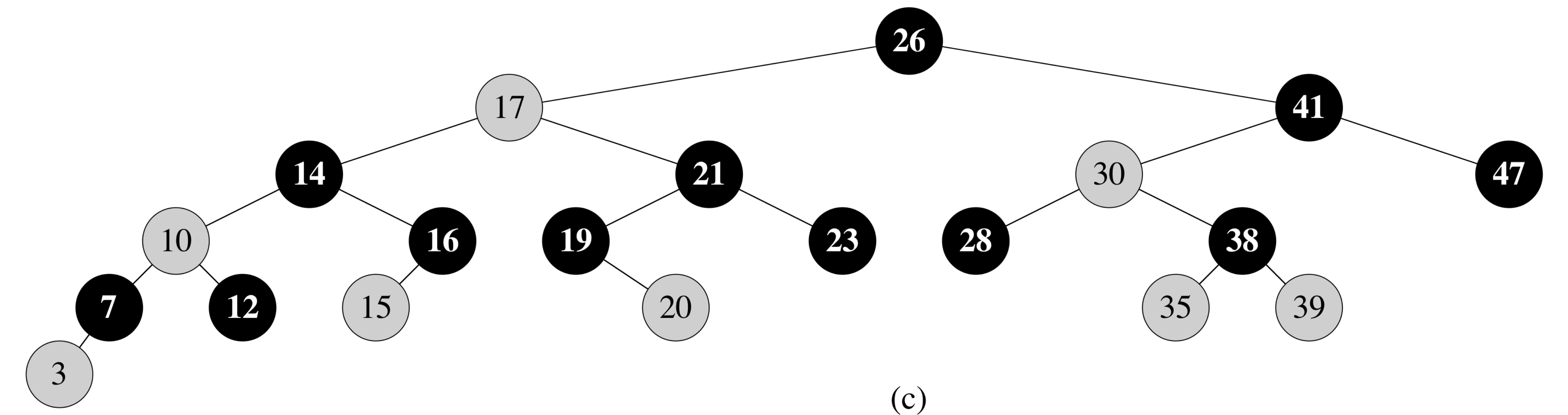
Limiting the Height of Red-Black Trees

Lemma: A red-black tree with n internal nodes has height at most 2⋅log(n+1)

Definiton: The black-height of a node x, denoted bh(x), is the number of black nodes on any simple path from, but not including, x down to a leaf.

Exercises

• The longest simple path from a node x in a red-black tree to a descendant leaf has length at most twice that of the shortest simple path from node x to a descendant leaf.
• What is the largest possible number of internal nodes in a red-black tree with black-height k? What is the smallest possible number?

Rotations

Does the search tree property continue to be satisfied after a rotation?

Can a rotation change the height of the tree?

Left-Rotate

  Left-Rotate (T, x)

  1   y = x.right                    // set x
  2   x.right = y.left               // turn y's subtree into x's right subtree
  3   if y.left ≠ T.nil
  4      y.left.p = x
  5   y.p = x.p                      // link x's parent to y
  6   if x.p == T.nil
  7      T.root = y
  8   elseif x == x.p.left
  9      x.p.left = y
 10   else x.p.right = y
 11   y.left = x                     // put x on y's left
 12   x.p = y
	

Rotations Example

Tree-Insert

  Tree-Insert (T, z)

  1   y = NIL
  2   x = T.root
  3   while x ≠ NIL
  4      y = x
  5      if z.key ≤ x.key
  6         x = x.left
  7      else x = x.right
  8      z.p = y
  9      if y == NIL
 10         T.root = z
 11      elseif z.key < y.key
 12         y.left = z
 13      else y.right = z
	

Tree Insert Example

RB-Insert

  RB-Insert (T, z)

  1   y = T.nil
  2   x = T.root
  3   while x ≠ T.nil
  4      y = x
  5      if z.key ≤ x.key
  6         x = x.left
  7      else x = x.right
  8      z.p = y
  9      if y == T.nil
 10         T.root = z
 11      elseif z.key < y.key
 12         y.left = z
 13      else y.right = z
 14   z.left = T.nil
 15   z.right = T.nil
 16   z.color = RED
 17   RB-Insert-Fixup(T, z)
		

  Tree-Insert (T, z)

  1   y = NIL
  2   x = T.root
  3   while x ≠ NIL
  4      y = x
  5      if z.key ≤ x.key
  6         x = x.left
  7      else x = x.right
  8      z.p = y
  9      if y == NIL
 10         T.root = z
 11      elseif z.key < y.key 
 12         y.left = z
 13      else y.right = z
		

RB-Insert-Fixup

  RB-Insert-Fixup (T, z)

  1   while z.p.color == RED
  2      if z.p == z.p.p.left
  3         y = z.p.p.right
  4         if y.color == RED
  5            z.p.color = BLACK           // case 1
  6            y.color = BLACK              // case 1
  7            z.p.p.color = RED            // case 1
  8            z = z.p.p                           // case 1
  9         else if z == z.p.right
 10               z = z.p                          // case 2
 11               Left-Rotate(T, z)       // case 2
 12            z.p.color = BLACK          // case 3
 13            z.p.p.color = RED           // case 3
 14            Right-Rotate(T, z.p.p)  // case 3
 15      else (same as then clause with
                     “right” and “left” exchanged)
 16   T.root.color = BLACK
	

Insert Fixup Example

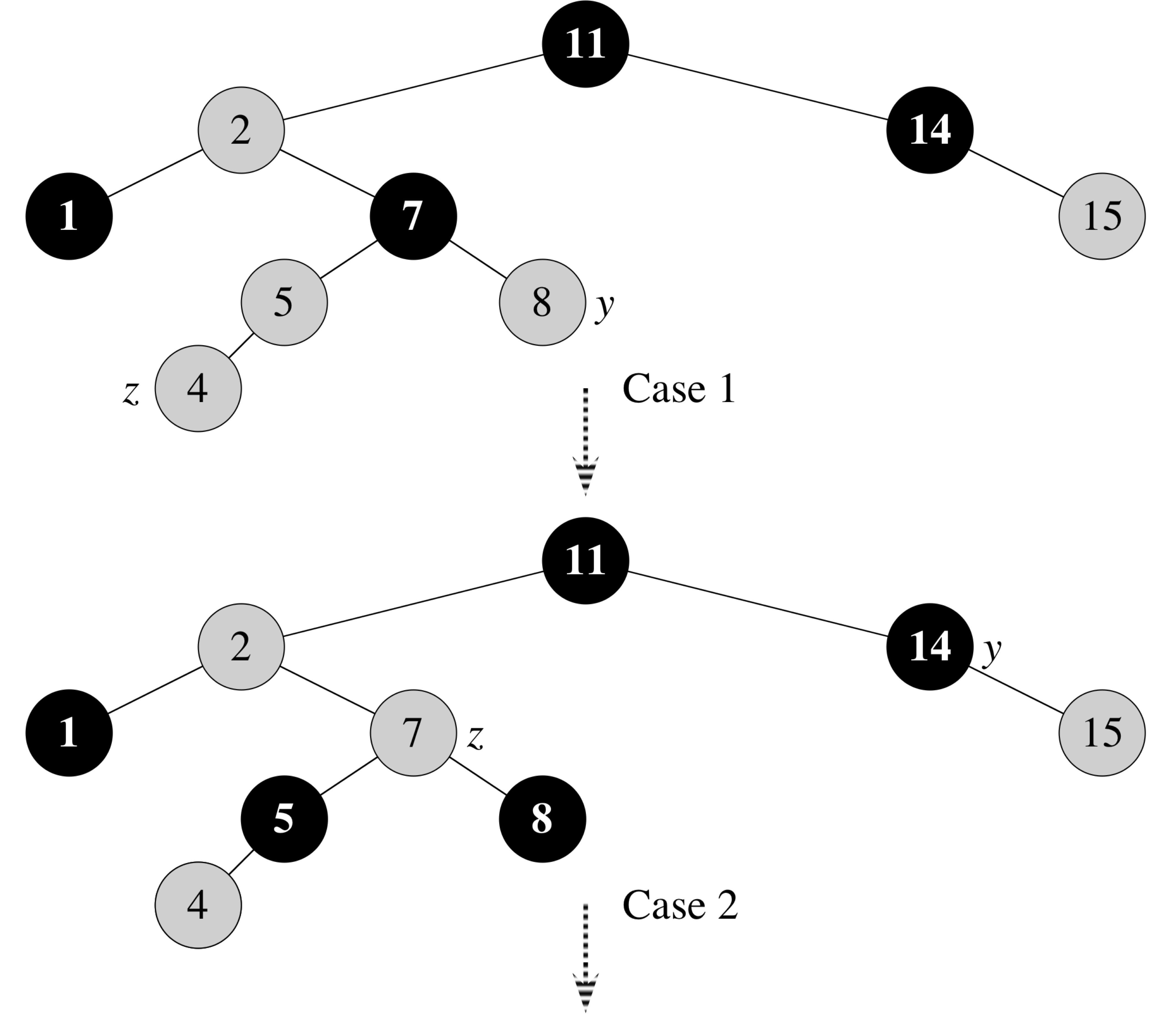
Insert Fixup Example

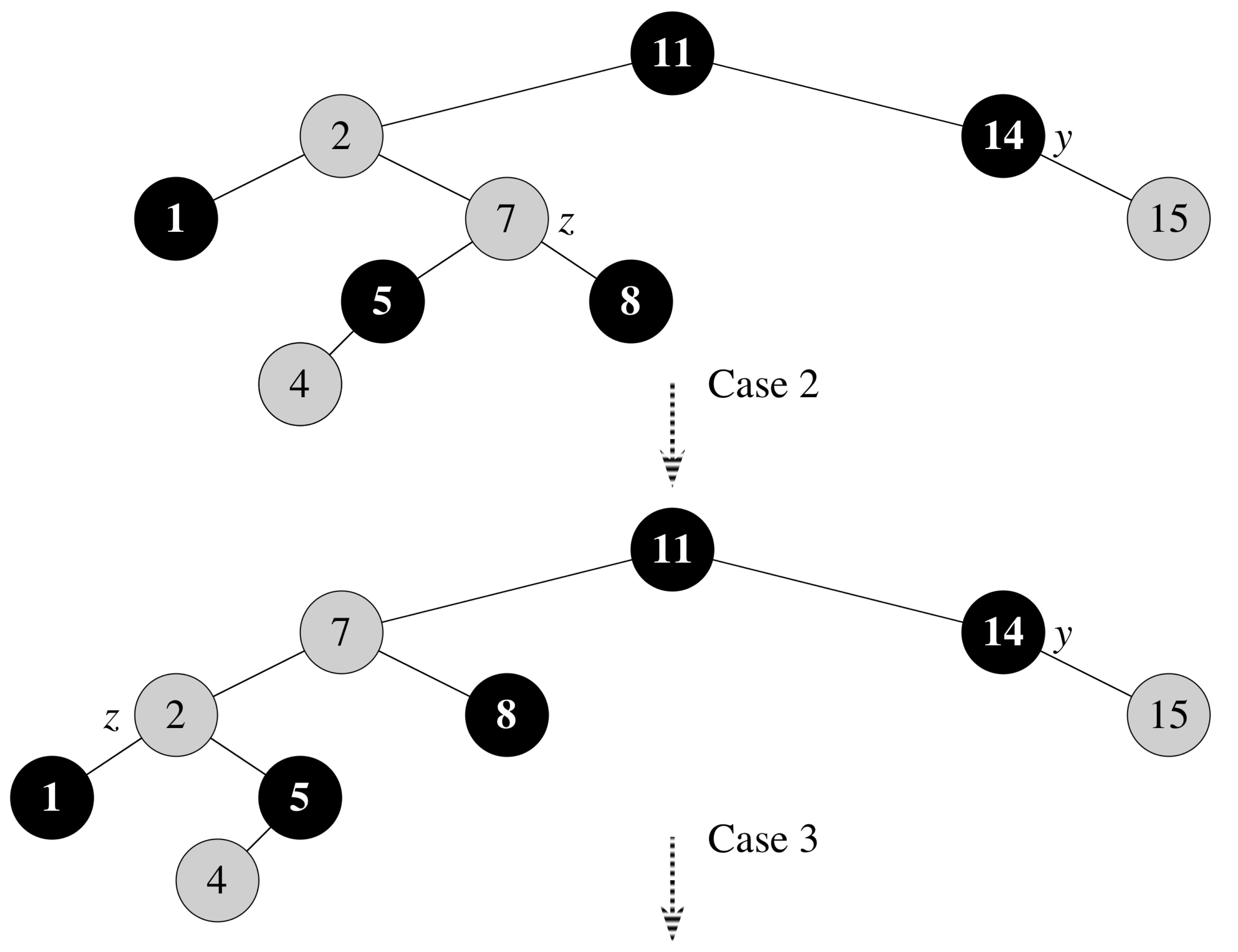
Insert Fixup Example

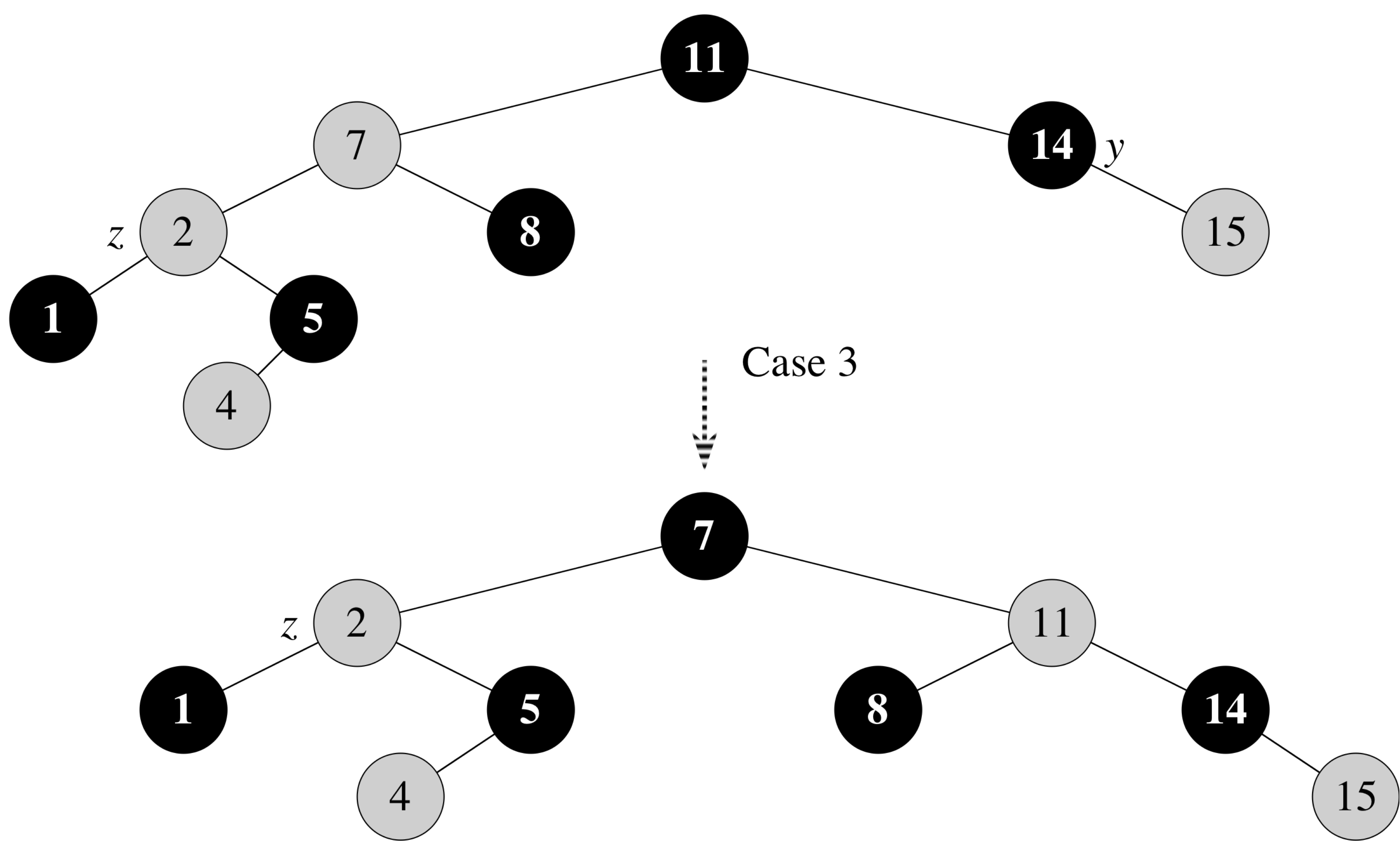
How does it Work?

Following invariants are satisfied:

• Node z is red
• If z.p is the root, then z.p is black
• If the tree violates any of the red-black properties, then it violates at most one of them, and the violation is either of property 2 or property 4
  • if the tree violates property 2, it is because z is the root and is red
  • If the tree violates property 4, it is because both z and z.p are red

Insert Fixup (Case 1)

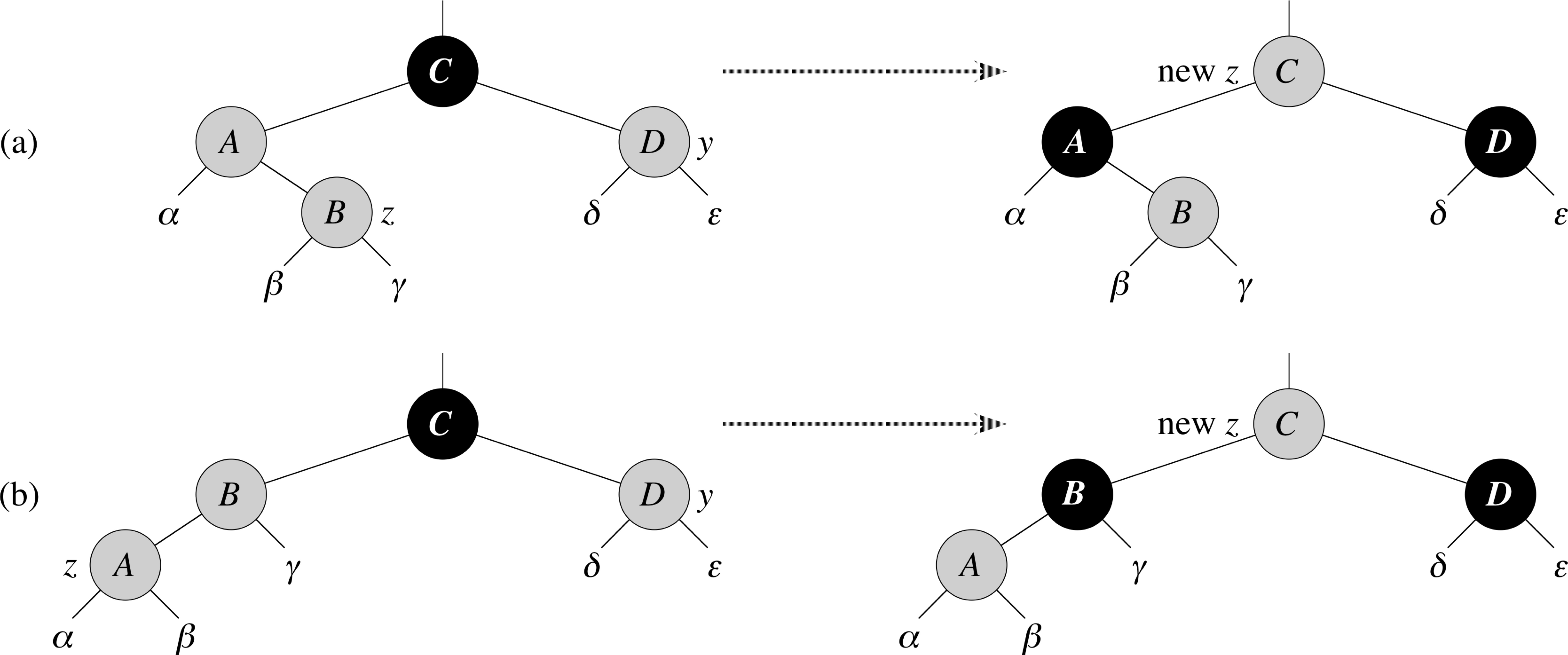
Insert Fixup (Cases 2 and 3)

Deletion from Search Tree

  Transplant (T, dst, src)

  1   if dst.p == NIL
  2      T.root = src
  3   elseif dst == dst.p.left
  4      dst.p.left = src
  5   else dst.p.right = src
  6   if src ≠ NIL
  7      src.p = dst.p
		

  Tree-Delete (T, z)

  1   if z.left == NIL
  2      Transplant(T, z, z.right)
  3   elseif z.right == NIL
  4      Transplant(T, z, z.left)
  5   else y = Tree-Minimum(z.right)
  6      if y.p ≠ z
  7         Transplant(T, y, y.right)
  8         y.right = z.right
  9         y.right.p = y
 10      Transplant(T, z, y)
 11      y.left = z.left
 12      y.left.p = y
		

Delete (Cases 1 and 2)

Delete (Case 3)

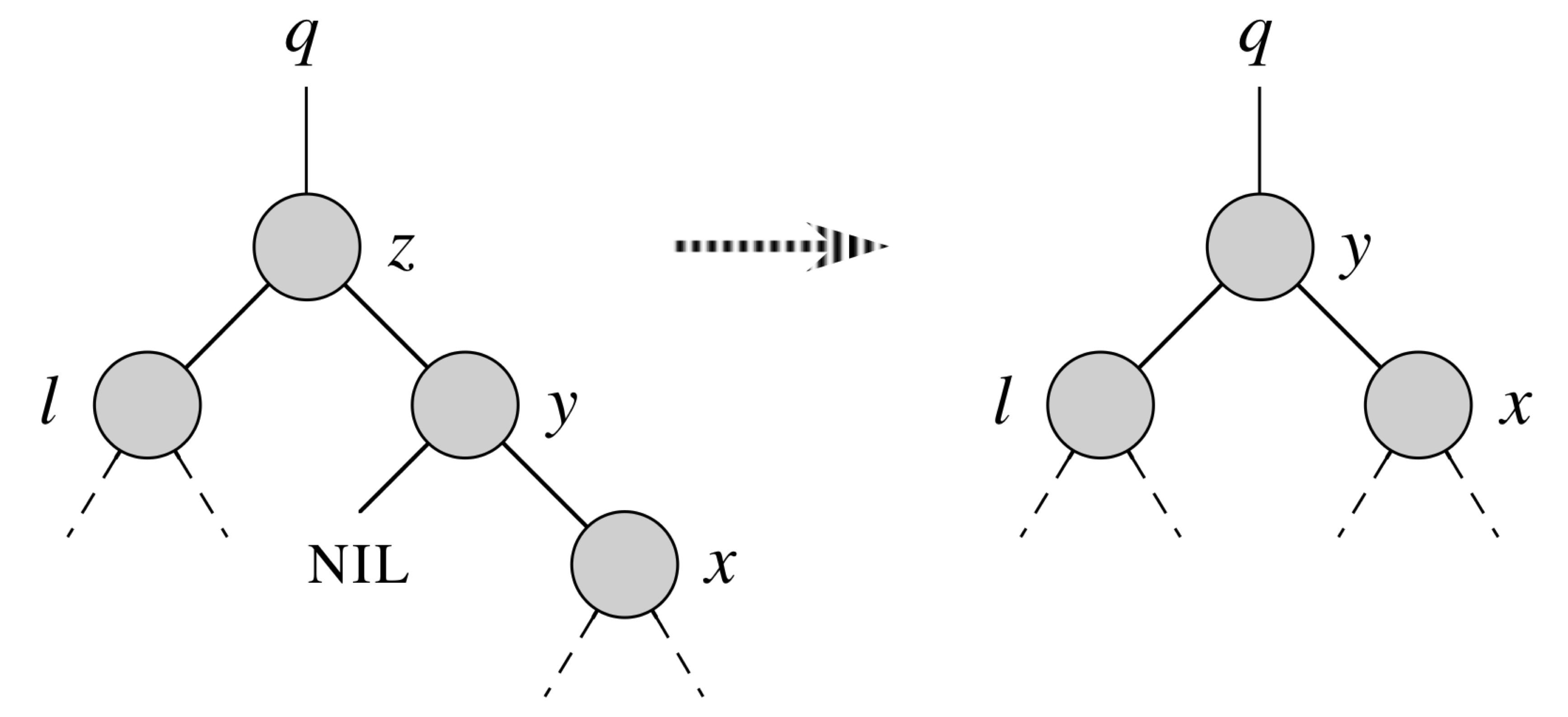
Delete (Case 4)

RB-Translplant

  RB-Transplant (T, dst, src)

  1   if dst.p == T.nil
  2      T.root = src
  3   elseif dst == dst.p.left
  4      dst.p.left = src
  5   else dst.p.right = src
 7    src.p = dst.p
		

  Transplant (T, dst, src)

  1   if dst.p == NIL
  2      T.root = src
  3   elseif dst == dst.p.left
  4      dst.p.left = src
  5   else dst.p.right = src
  6   if src ≠ NIL
  7      src.p = dst.p
		

Deletion from Red-Black Search Tree

  RB-Delete (T, z)

  1   y = z
  2   y-original-color = y.color
  3   if z.left == T.nil
  4      x = z.right
  5      RB-Transplant(T, z, z.right)
  6   elseif z.right == T.nil
  7      x = z.left
  8      RB-Translplant(T, z, z.left)
  9   else y = Tree-Minimum(z.right)
 10      y-original-color = y.color
 11      x = r.right
 12      if y.p == z
 13         x.p = y
 14      else RB-Transplant(T, y, y.right)
 15         y.right = z.right
 16         y.right.p = y
 17      RB-Transplant(T, z, y)
 18      y.left = z.left
 19      y.left.p = y
 20      y.color = z.color
 21   if y-original-color == BLACK
 22      RB-Delete-Fixup(T, x)      
		

 Tree-Delete (T, z)

  1   if z.left == NIL
  2      Transplant(T, z, z.right)
  3   elseif z.right == NIL
  4      Transplant(T, z, z.left)
  5   else y = Tree-Minimum(z.right)
  6      if y.p ≠ z
  7         Transplant(T, y, y.right)
  8         y.right = z.right
  9         y.right.p = y
 10      Transplant(T, z, y)
 11      y.left = z.left
 12      y.left.p = y
		

RB-Delete-Fixup

  RB-Delete-Fixup (T, x)

  1   while x ≠ T.root and x.color == BLACK
  2      if x == x.p.left
  3         w = x.p.right
  4         if w.color == RED
  5-8          // CASE 1
  9         if w.left.color == BLACK and w.right.color == BLACK
 10-11         // CASE 2
 12         else if w.right.color == BLACK
 13-16         // CASE 3
 17-21         // CASE 4
 22      else (same as then clause with “right” and “left” exchanged)
 23   x.color = BLACK
 
	

RB-Delete-Fixup: Case 1

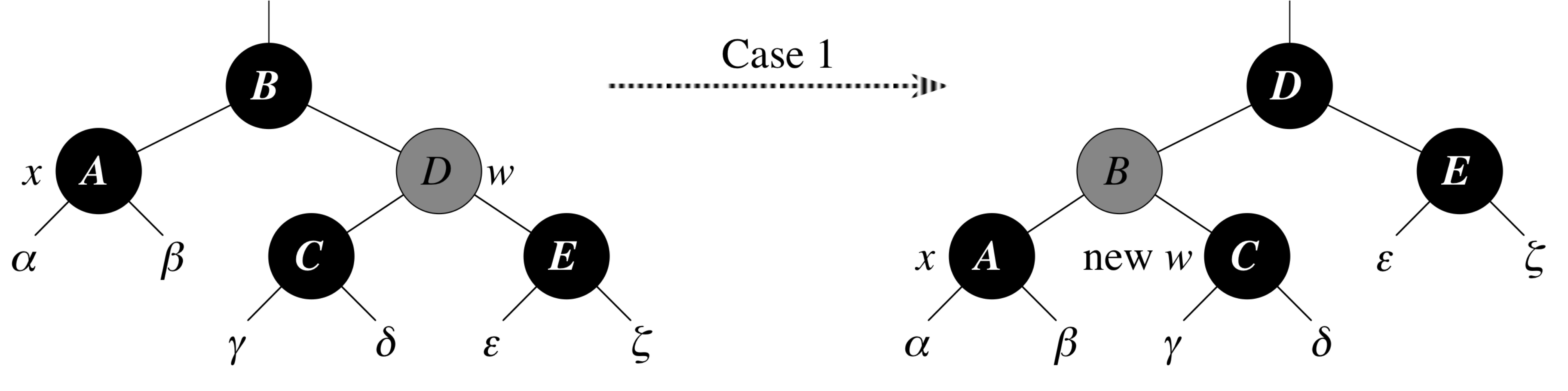
x's sibling w is red

RB-Delete-Fixup: Case 2

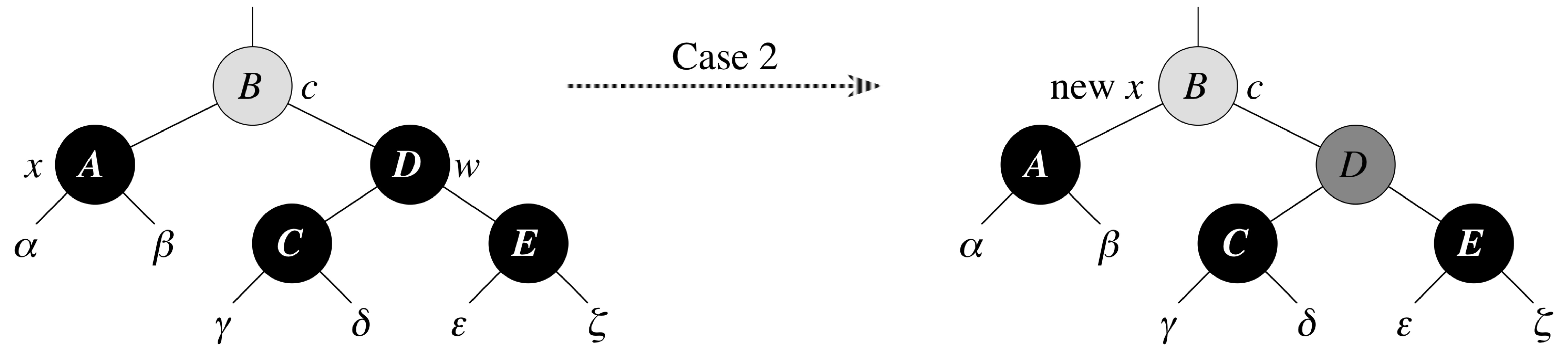
x's sibling w is black and both of w's children are black

RB-Delete-Fixup: Case 3

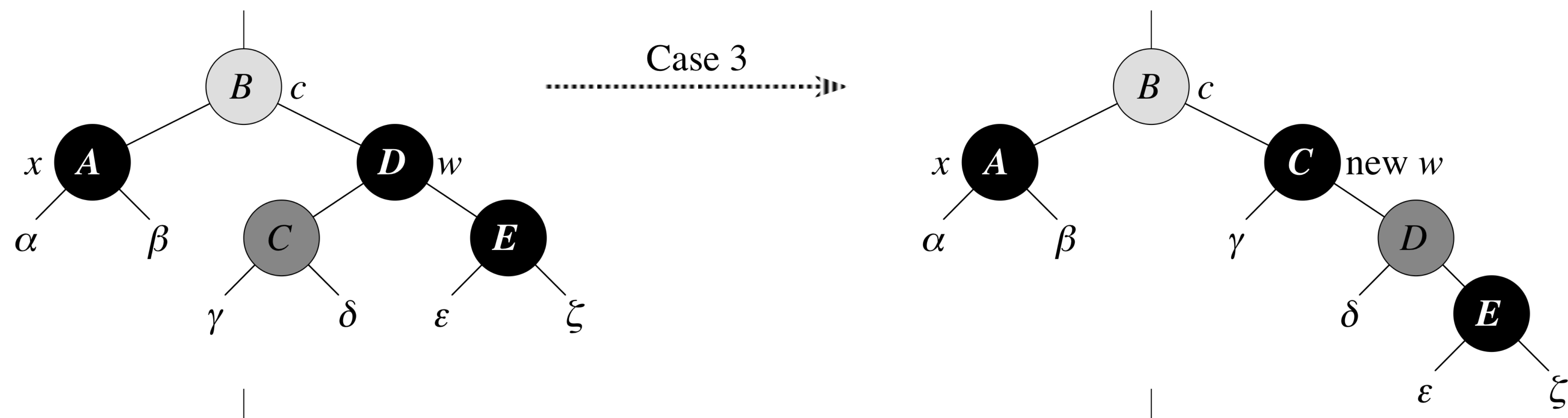
x's sibling w is black, w's left child is red, and w's right child is black

RB-Delete-Fixup: Case 4

x's sibling w is black, w's left right is red

Augmenting Red-Black Trees

• Dynamic order statistics
  • quick order statistics in a dynamic list
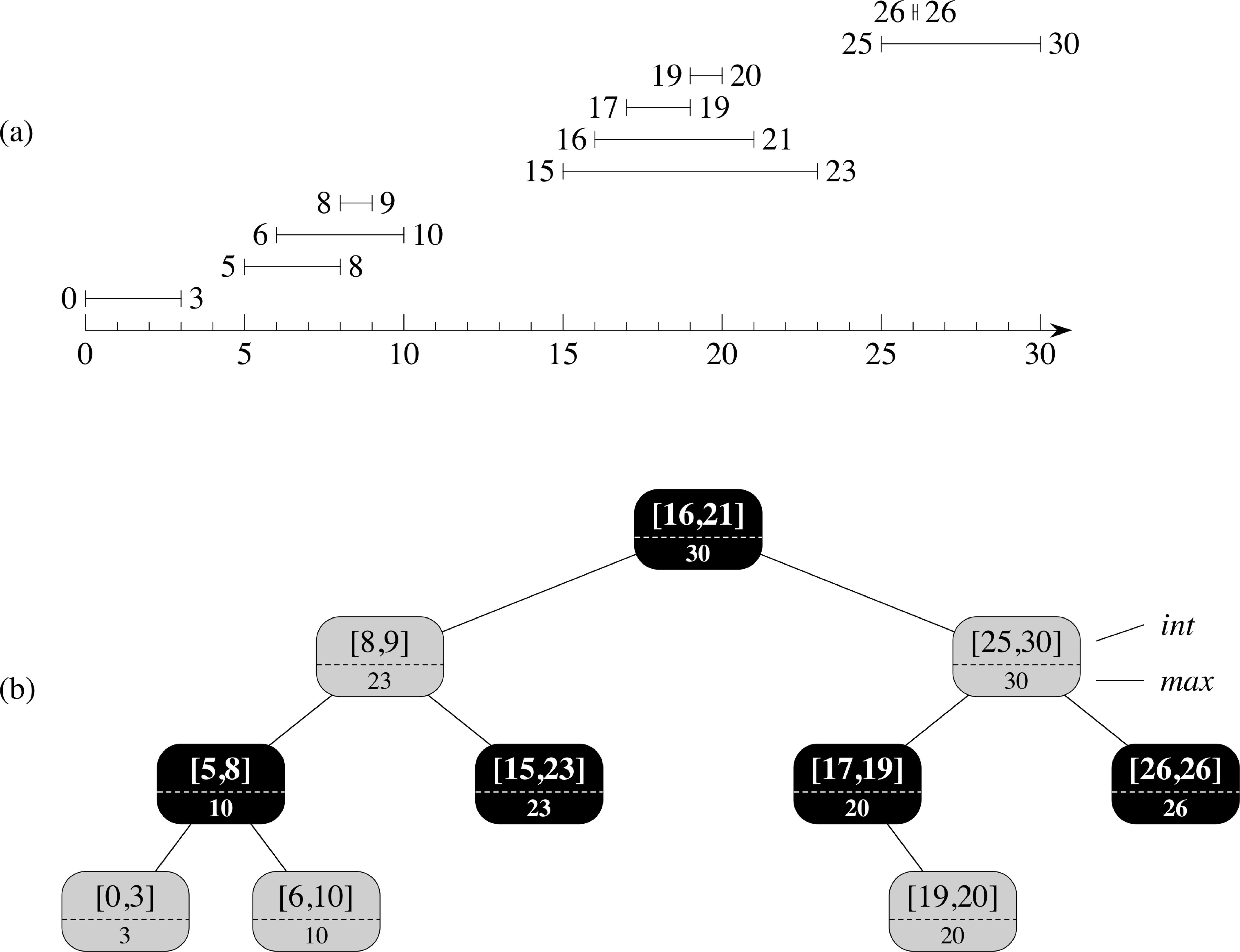
• Interval Trees
  • quickly determining conflicting intervals

Where might you use interval trees?

Dynamic Order Statistic

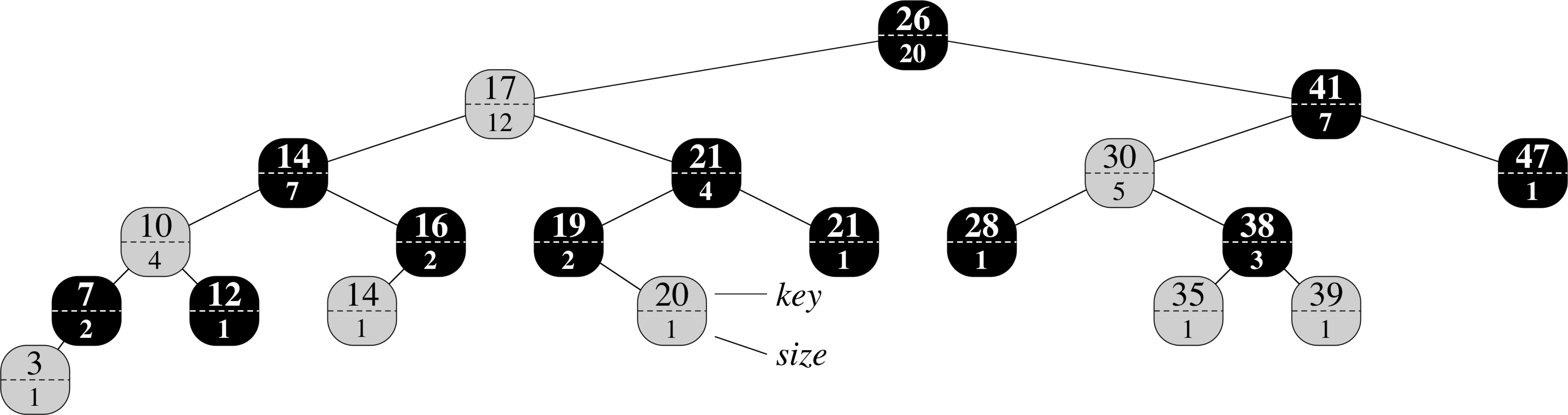
Dynamic Order Statistic: Tree Update

Interval Trees